A hollow uncharged spherical conductor has inner radius A and outer radius b. A positive point charge +q is in the cavity at the center of the sphere (Fig. 3.48). Find the potential V( r) everywhere, assuming that V=0 at r→∞.
 .
.
The conductor is an equipotential volume, so V is constant for a≤r≤b. The field lines inside the cavity must end on the inner surface of the cavity, so this surface has an induced charge −q. Since the shell is uncharged a positive charge +q is on the outer surface (Fig . 3.49).
 .
.
The three charges q at the center, −q on the inner surface, and +q on the outer surface produce a field
Er=14πε0qr2
for r>b, so the potential for r>b is
V=14πε0qr
Outside the shell, V(r) is the same as that due to a point charge q at the origin. Choosing V=0 at r=∞, we have
V(r)=14πε0qr,r≥b
At r = b, the potential is q/4πε0b,Vremains at this constant value throughtout the spherical shell from r=b to r=a, so
V(r)=14πε0qb,a≤r≤b
For any point inside the cavity (r<a)
V ( r) = Electric potential due to q at center + Electric potential due charge distributed on spherical surface of radius a + Electric potential due to charge distributed on spherical surface of radius B. So
V(r)=Vq+Va,inside+Vb,outside
=14πε0qr+14πε0(−q)a+14πε0qb
=14πε0qr+14πε0qb−14πε0qa,r≤a
(Figure 3.50) shows the electric potential as a function of distance from the center of the cavity.
 ,
,
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Examples
9 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.1
23 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
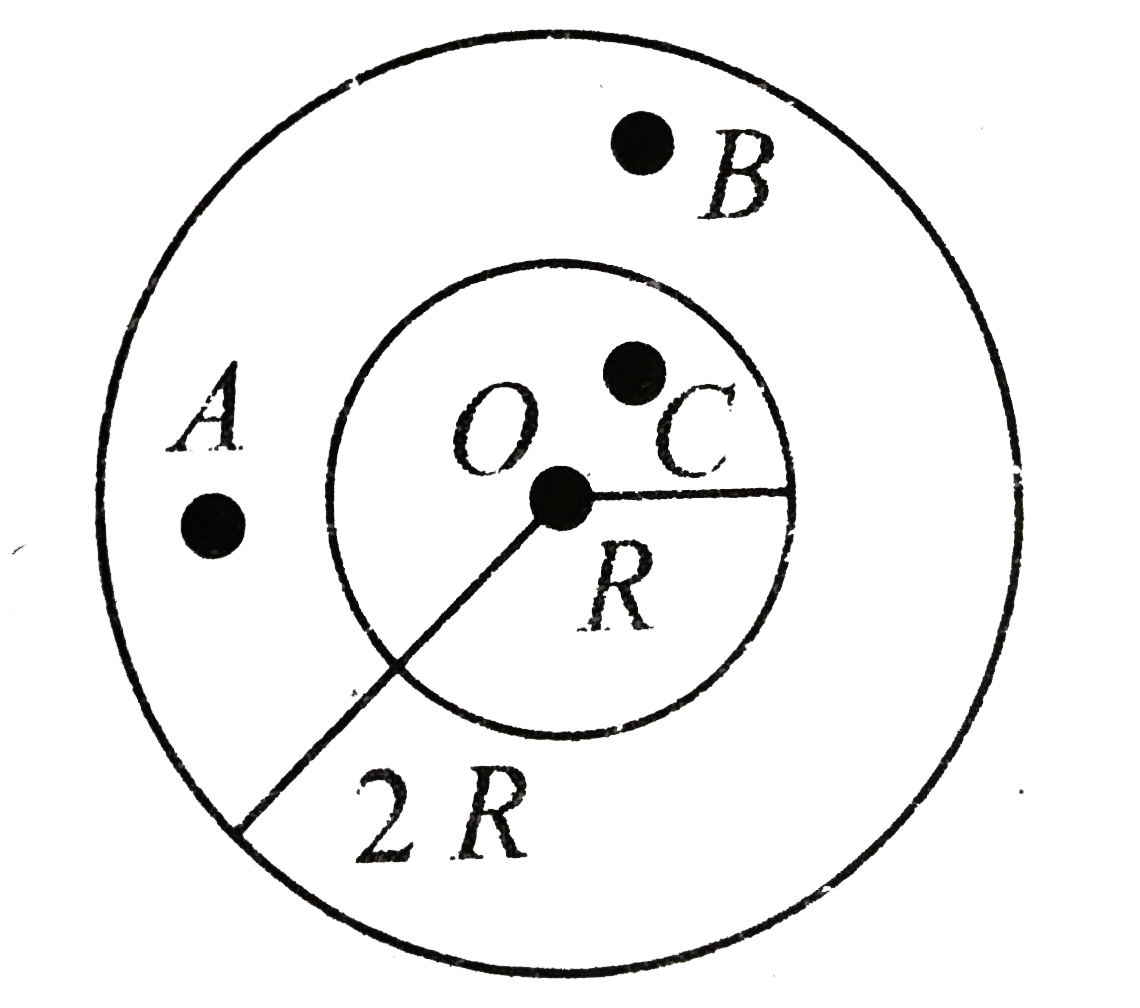
A hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the
View SolutionA metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is
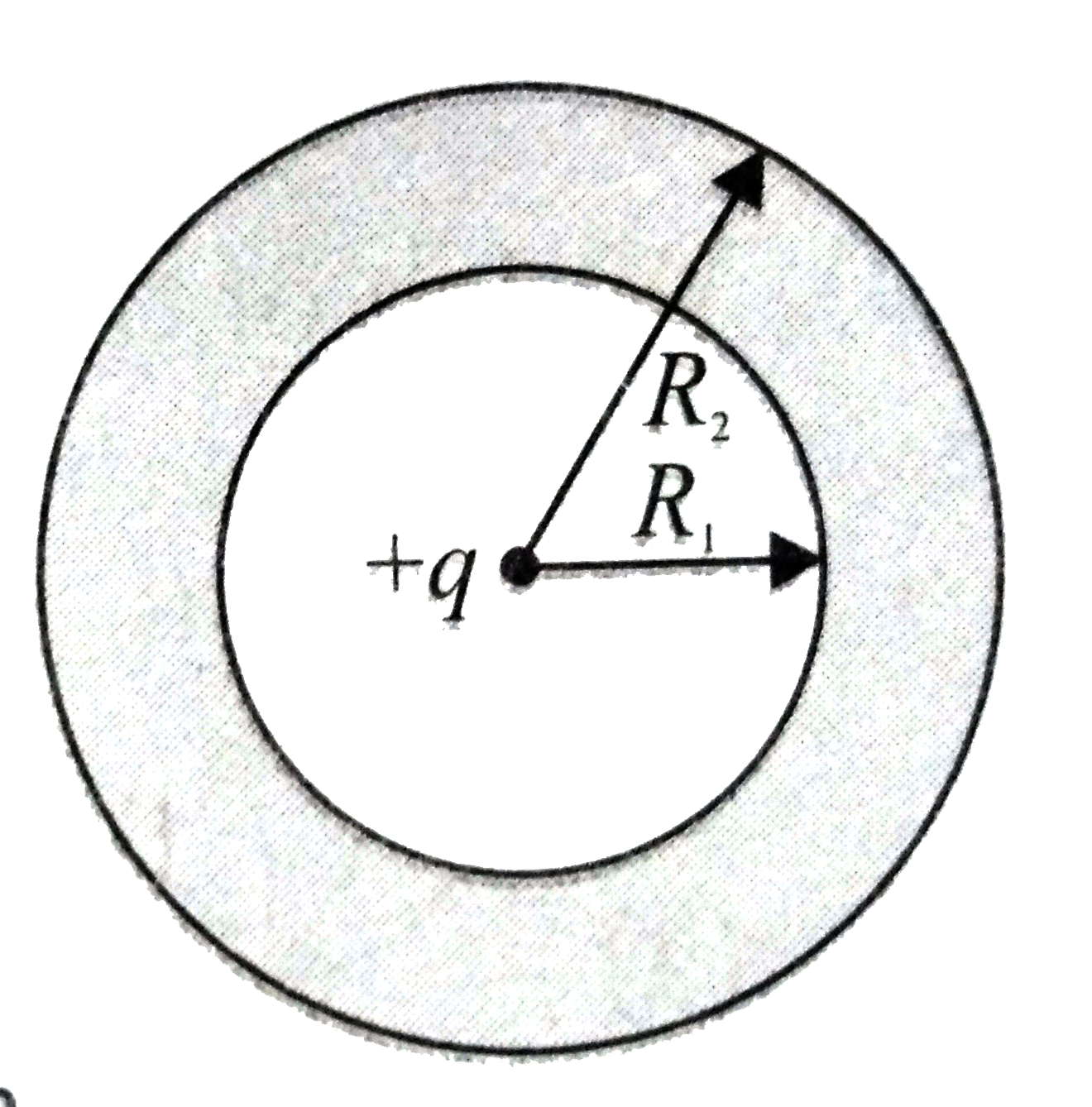
View SolutionA metal spherical shell has an inner radius R1 and outer radius R2. A charge Q is placed at the center of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface ?
View SolutionInside a conducting hollow sphere of inner radius R1 and outer radius R2, a point charge q is placed at a distance x from the center as shown in fig. Find.
 .
.
(i) electric potential at C
(ii) electric field and potential at a distance r from the center outside the shell.
View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionA point charge Q is placed inside a conducting spherical shell of inner radius 3R and outer radius 5R at a distance R from the centre of the shell. The electric potential at the centre of the shell will be
View SolutionA charge Q is kept at the centre of a conducting sphere of inner radius R1 and outer radius R2. A point charge q is kept at a distance r(>R2) from the centre. If q experiences an electrostatic force 10 N then assuming that no other charges are present, electrostatic force experienced by Q will be :
View SolutionA solid, uncharged conducting sphere of radius 3a contains a concentric hollowed spherical cavitiy of radius a.
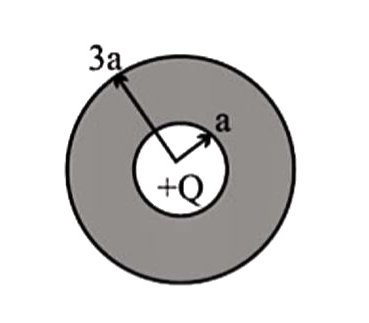
A point charge +Q is placed at the center of the spheres. Taking V=0 at r→∞, the potential at positiion r=2a from the center is-
View SolutionA solid spherical conductor of radius R has a spherical cavity of radius at its centre. A charge is kept at the centre. The charge at the inner surface, outer surface are respectively.
View SolutionAn uncharged conductor of inner radius R1 and outer radius R2 constains a point charge q at the centre as shown in figure
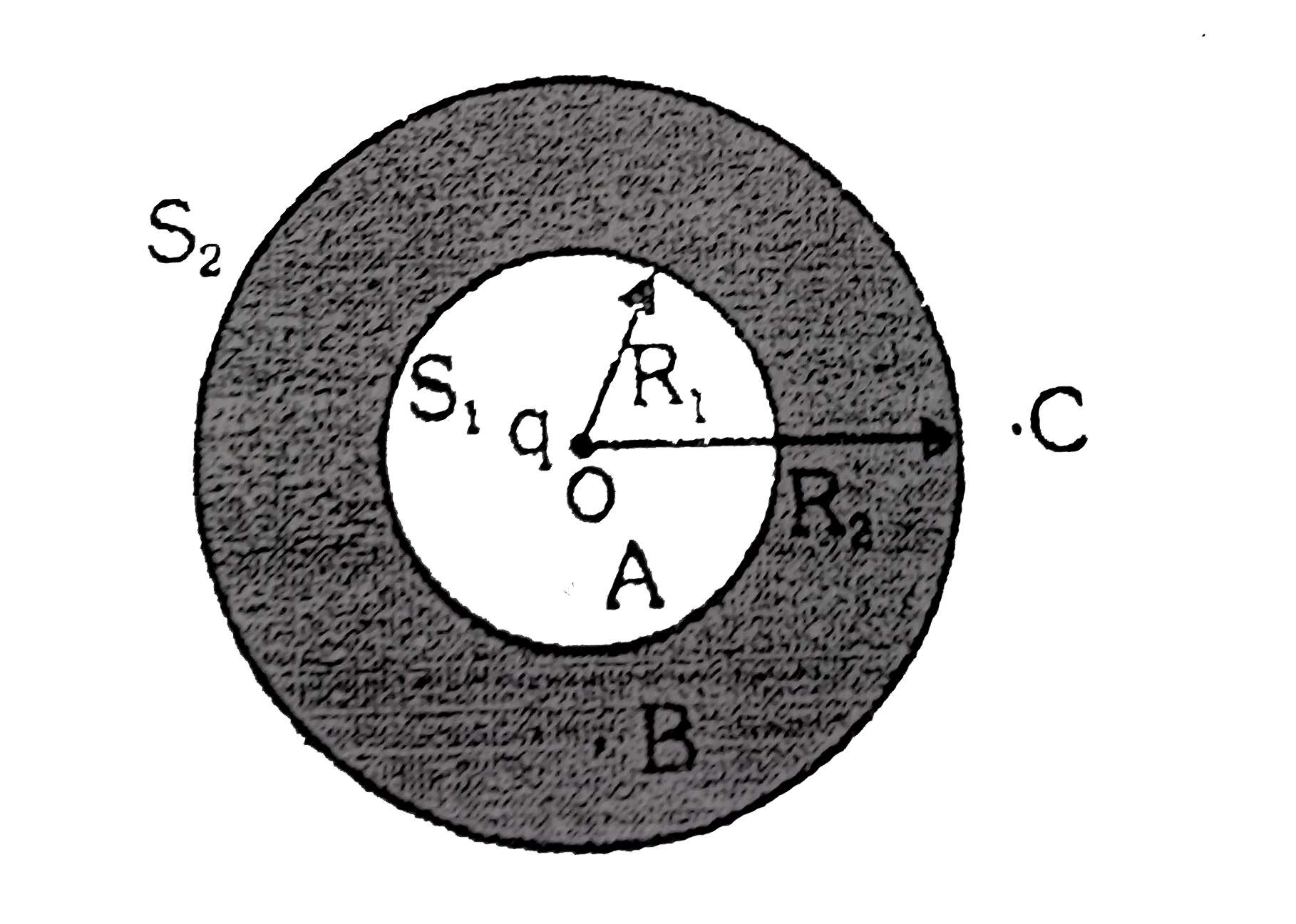
(i) Find →E and V at points A, B and C
(ii) If a pint charge Q is kept out side the sphere at a distance 'r'(>>R2) from centre then find out resultant force on charge Q and charge q.
View Solution
