A metal spherical shell has an inner radius R1 and outer radius R2. A charge Q is placed at the center of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface ?
To solve the problem, we need to determine the surface charge density on the inner and outer surfaces of a metal spherical shell when a charge Q is placed at the center of the spherical cavity.
1. Understanding the Setup:
- We have a metal spherical shell with an inner radius R1 and an outer radius R2.
- A charge Q is placed at the center of the spherical cavity.
2. Induced Charge on the Inner Surface:
- The presence of the charge Q at the center will induce a charge on the inner surface of the spherical shell.
- Since the shell is neutral and the charge Q is positive, an equal and opposite charge will be induced on the inner surface. Therefore, the induced charge on the inner surface will be −Q.
3. Induced Charge on the Outer Surface:
- The total charge on the shell must remain zero. Therefore, if −Q is induced on the inner surface, a charge of +Q will be induced on the outer surface of the shell.
4. Calculating Surface Charge Density on the Inner Surface:
- The surface charge density σ1 on the inner surface is given by the formula:
σ1=Charge on inner surfaceArea of inner surface
- The area of the inner surface (which is a sphere) is 4πR21.
- Therefore, the surface charge density on the inner surface is:
σ1=−Q4πR21
5. Calculating Surface Charge Density on the Outer Surface:
- The surface charge density σ2 on the outer surface is given by:
σ2=Charge on outer surfaceArea of outer surface
- The area of the outer surface is 4πR22.
- Therefore, the surface charge density on the outer surface is:
σ2=Q4πR22
Final Answers:
- (i) The surface charge density on the inner surface is:
σ1=−Q4πR21
- (ii) The surface charge density on the outer surface is:
σ2=Q4πR22
- We have a metal spherical shell with an inner radius R1 and an outer radius R2.
- A charge Q is placed at the center of the spherical cavity.
- The presence of the charge Q at the center will induce a charge on the inner surface of the spherical shell.
- Since the shell is neutral and the charge Q is positive, an equal and opposite charge will be induced on the inner surface. Therefore, the induced charge on the inner surface will be −Q.
- The total charge on the shell must remain zero. Therefore, if −Q is induced on the inner surface, a charge of +Q will be induced on the outer surface of the shell.
- The surface charge density σ1 on the inner surface is given by the formula:
σ1=Charge on inner surfaceArea of inner surface
- The area of the inner surface (which is a sphere) is 4πR21.
- Therefore, the surface charge density on the inner surface is:
σ1=−Q4πR21
- The surface charge density σ2 on the outer surface is given by:
σ2=Charge on outer surfaceArea of outer surface
- The area of the outer surface is 4πR22.
- Therefore, the surface charge density on the outer surface is:
σ2=Q4πR22
- (i) The surface charge density on the inner surface is:
σ1=−Q4πR21
- (ii) The surface charge density on the outer surface is:
σ2=Q4πR22
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - B
7 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - C
10 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
A metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is

View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the center of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?
(b) Is the electric field intensity inside a cavity (with no charge) zero, even if the shell is not spherical, but has any irregular shape ? Explain.
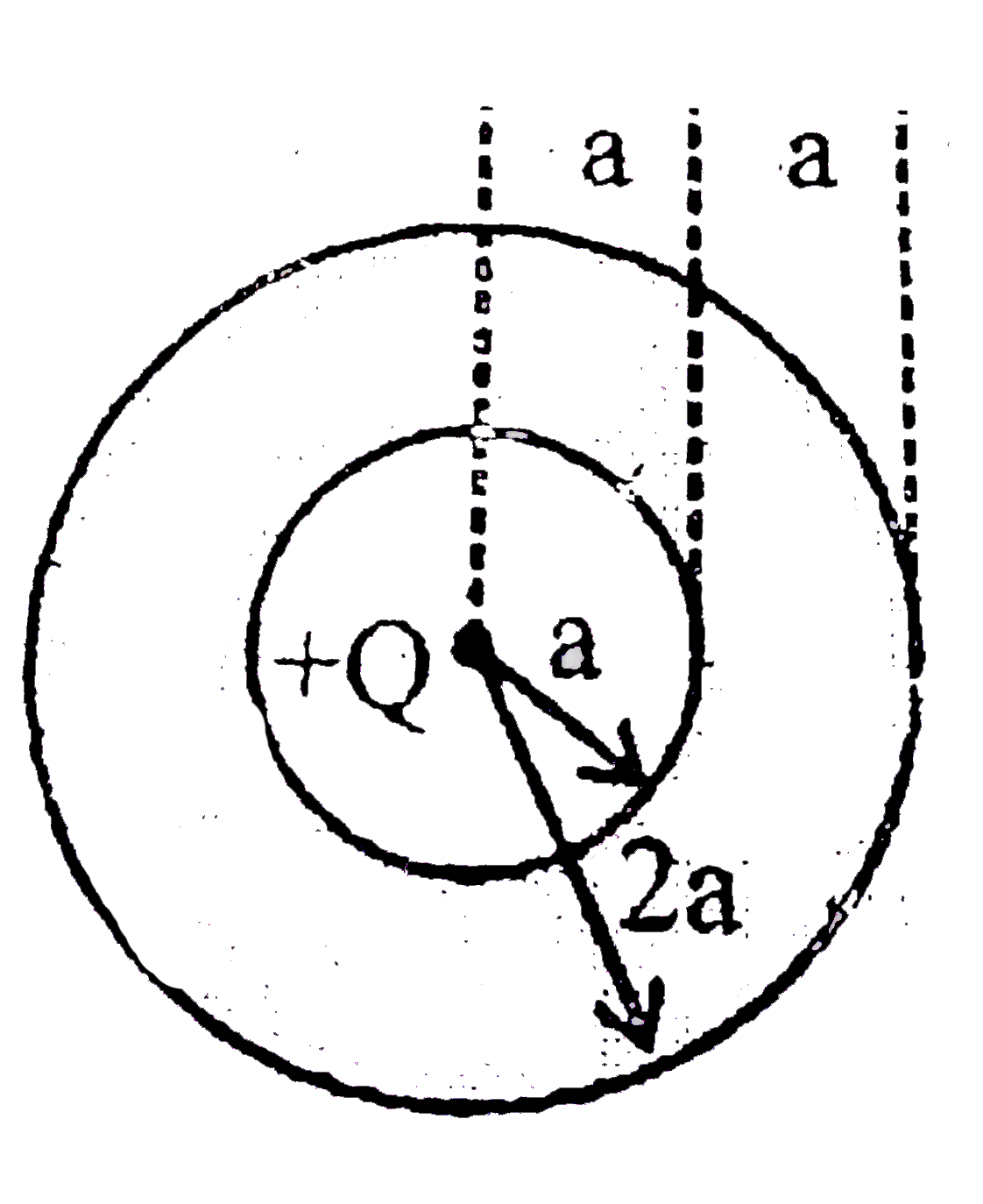
View SolutionA solid spherical conducting shell has inner radius a and outer radius 2a. At the center of the shell is located a point charge +Q. What must the excess charge of the shell be in order for the charge density on the inner and outer surface of the shell to be exactly equal?
View SolutionA ball with charge −50e is placed at the centre of a hollow spherical shell has a net charge of −50e. What is the charge on the shell's outer surface ?
View SolutionShown in the figure a spherical shell with an inner radius 'a' and an outer radius 'b' is made of conducting metarial. A charge +Q is placed at the centre of the spherical shell and a total charge -q s placed on the shell. Charge -q is districuted on the surfaces as :

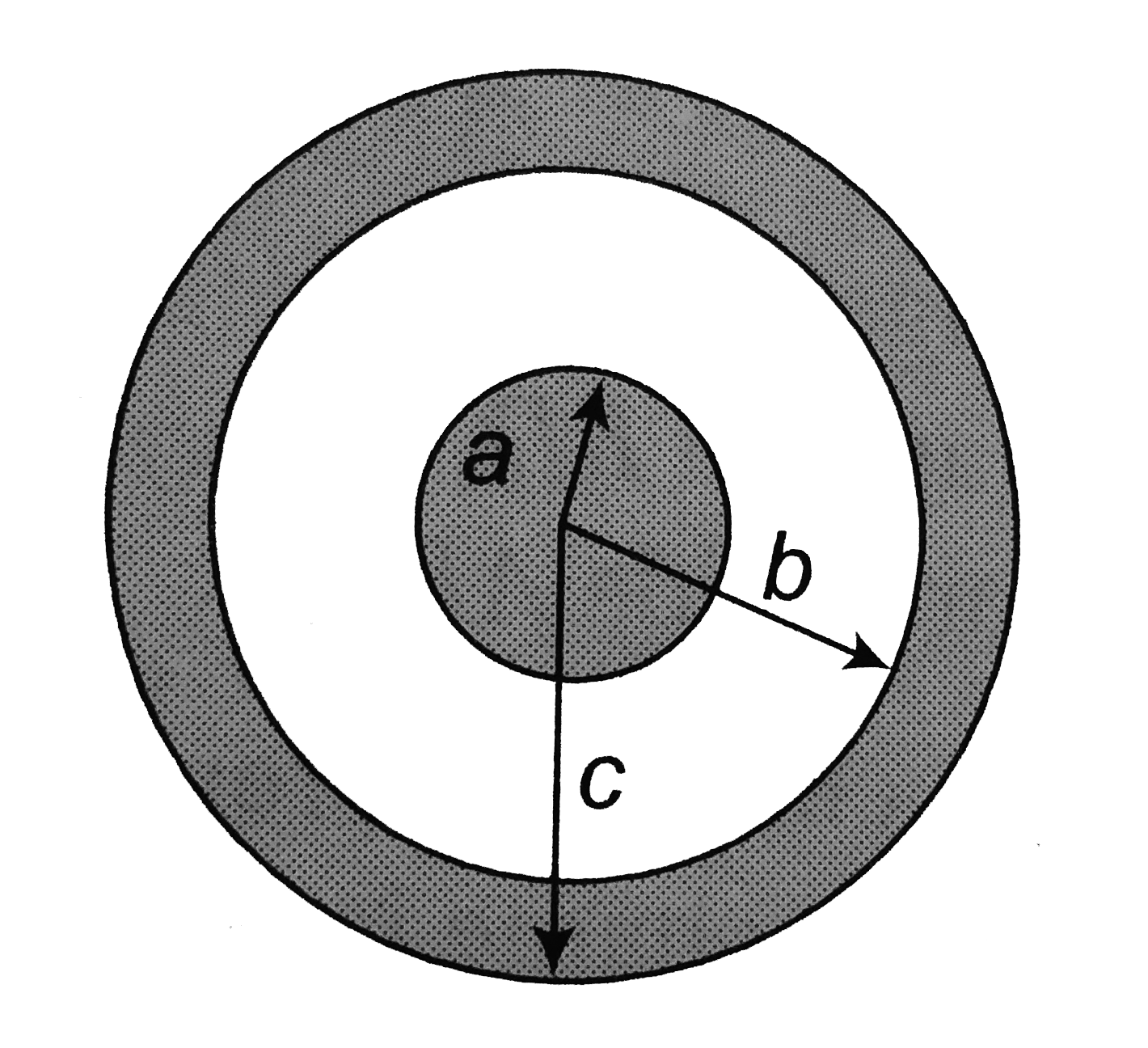
View SolutionA solid conducting sphere of radius a has a net positive charge 2Q. A conducting spherical shell of inner radius b and outer radius c is concentric with the solid sphere and has a net charge −Q. The surface charge density on the inner and outer surfaces of the spherical shell will be
View SolutionA charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius alpha. (a) Find the surface charge density on the inner surface and on the outer surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and the outer surface?
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d. The inner shell has total charge +2q and the outer shell has charge +4q.
(i) What is the total charge on the (a) inner surface of the small shell, (b) outer surface of the small shell (c) inner surface of the large shell, (d) outer surface of the large shell ?
(ii) Calculate the electric field in terms of q and the the distance r from the common centre of two shells for (a) r<a, (b) a<r<b, (c) b<r<c, (d) c<r<d, (e) r>d

View SolutionA charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius a. (a) Find the surface charge density on the inner surface and on the outer surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and the outer surface? (c) Find the electric field inside the sphere at a distance x from the centre in the situations (a) and (b).
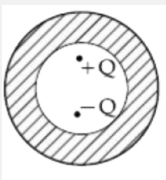
View SolutionShow in the figure are two point charge + Q and - Q inside the cavity of the Spherical .shell the changes are kept near the surface of the cavity on opposite sides of the centre of the shell if σ1 is the surface charge on the inner surface and Q1 net charge on it and σ2 the surface charge on the outer surface and Q2 net charge on it then :
View Solution
