A horizontal force F acts on the sphere at its centre as shown. Coefficient of friction between ground and sphere is μ. What is maximum value of F for which there is no slipping?

F−f=Ma ..(i)
τ=Iα=I(αR)
⇒f.R=25MR2aR
⇒f=25Ma
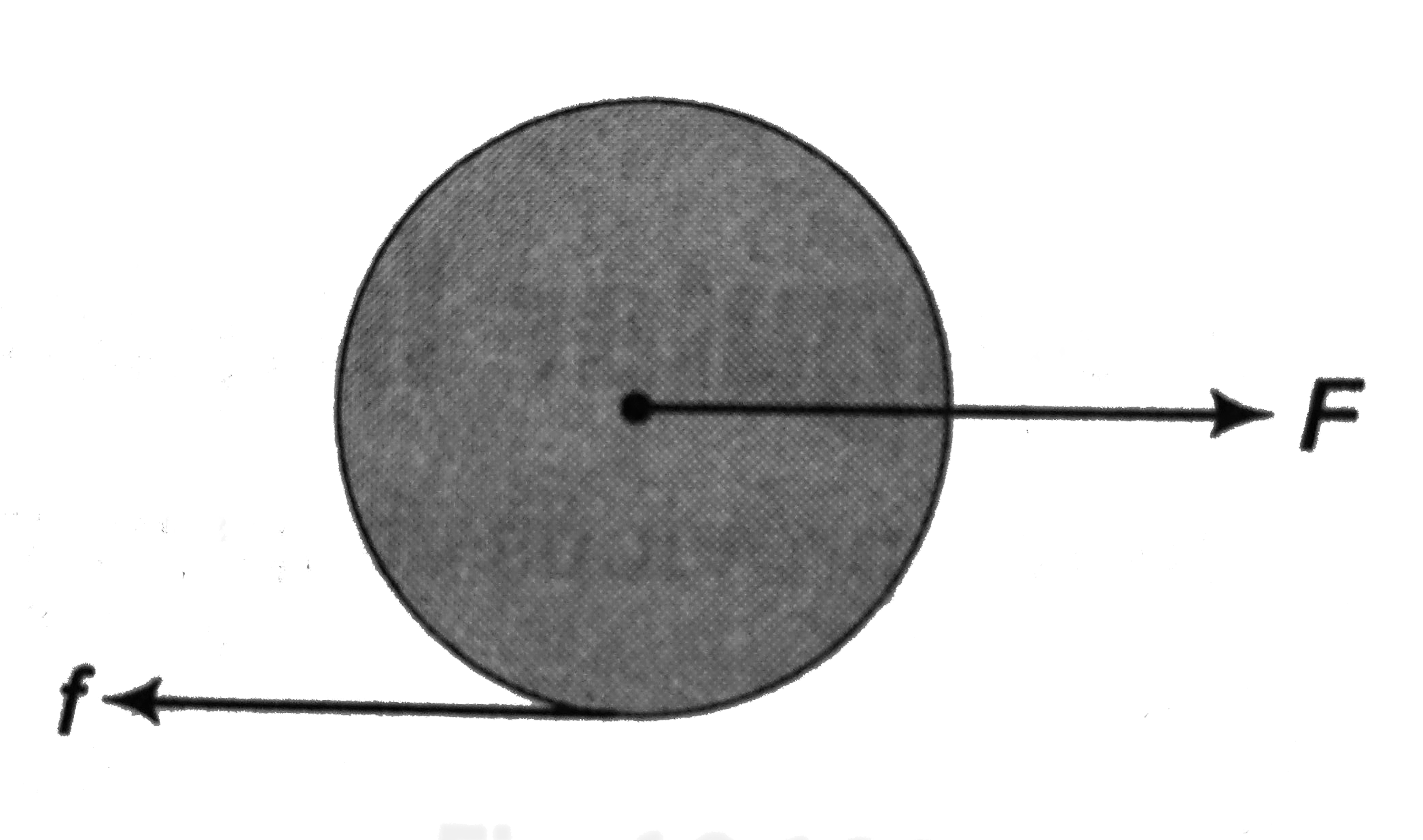
Solving Eqs. (i) and (ii) we get
f=27F
27F≤μmg
⇒F≤72μmg
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Examples25videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
Two hemispheres of radii R and r(<R) are fixed on a horizontal table touching each other (see figure). A uniform rod rests on to spheres as shown. The coefficient of friction between the rod and two spherers is μ. Then the maximum value of the ratio rR for which the rod will not slide is :
 View Solution
View SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to
 View Solution
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

A Horizontal force F is applied on the plank. What is the maximum value of F, if μ is coefficient of friction between sphere movment and plank and there is no slipping ?View SolutionA solid sphere of mass 2kg is pulled by a constant force acting at its centre on a rough surface having co-efficient of friciton 0.5. The maximum value of F so that the sphere rolls without slipping is
 View Solution
View SolutionCoefficient of friction between A and B is μ . The minimum force F with which A will be pushed such that B will not slip down is -
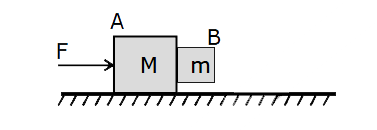 View Solution
View SolutionFour block are arranged on a smooth horizontal surface as shown in figure .The masses of the blocks are given (see the fig ) The coefficient of static friction between the top and the bottom blocks is μs What is the maximum value of the horizontal force F applied to one of the bottom blocks as shown that makes all four block with the same acceleration ?
 View Solution
View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?
 View Solution
View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?
 View Solution
View SolutionA force F is applied on the top of a cube as shown in the figure. The coefficient of friction between the cube and the ground is μ. If F is gradually increased, find the value of μ for which the cube will topple before sliding.
 View Solution
View SolutionIn the figure shown, a solid sphere of mass 'm' and radius r is released from a height 6r to slide down a smooth surface. A plank of same mass 'm' touches the horizontal portion of the surface at the ground. The co-efficient of friction between the plank and the sphere is μ and that between the plank and the ground is μ/4. Find the work done by the friction force between the plank and the ground till the sphere starts pure rolling on the plank. Neglect the height of the plank.
 View Solution
View Solution

