Question

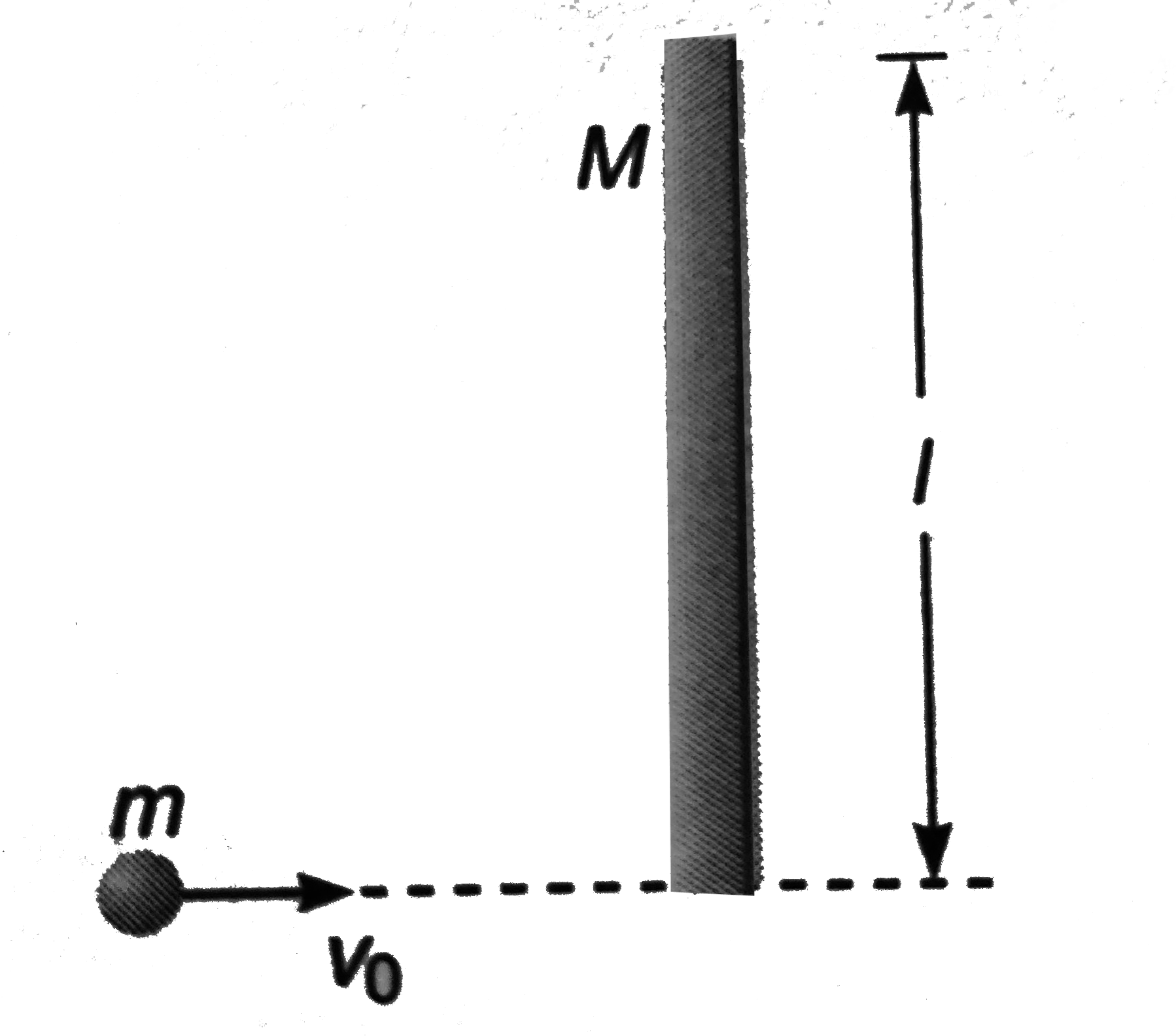
A boy mass m runs on ice with velocity $v^{}$ and steps on the end of a plank of length $l$ and mass $M$ which is perpendicular to his path.
(a). Describe quantitatively the motion of the system after the boy is on the plank. Neglect friction with the ice.
(b). One point on the plank is at rest immediately after the collision. Where is it?

Explanation

C is the COM of `(M+m)`
`BC=((M)/(M+m))(l)/(2)` ltbr and `OC=((m)/(M+m))((l)/(2))`
from conservation of linear momentum,
`(M+m)v=mv_(0)`
or `v=((m)/(M+m))v_(0)` .(i)
From conservation of angular momentum about point C we have
`mv_(0)(BC)=Iomega`
or `(mMv_(0)l)/(2(M+m))=[m((M)/(M+m))^(2)((l)/(4))^(2)+(Ml^(2))/(12)+M((m)/(M+m))^(2)((l^(2))/(4))]omega`
putting `(mv_(0))/(M+m)=v`
From Eq (i) we have
`(v)/(omega)=(l)/(6)[(4m+M)/(M+m)]`
Now a point say P at a distance `x=(v)/(omega)`, from C
(tawards O) will be at rest Hence distance of point P from by at B will be
`BP=BC+x`
`=((M)/(M+m))((l)/(2))+(l)/(6)[(4m+M)/(M+m)]`
`=(2l)/(3)`