A horizontal spring block system of mass M executes simple harmonic motion. When the block is passing through its equilibrium position, an object of mass m is put on it and the two move together. Find the new amplitude and frequency of vibration. Given, k is the spring constant of the system.
To solve the problem of a horizontal spring block system where an additional mass is placed on the block when it is at its equilibrium position, we will follow these steps:
1. Identify Initial Parameters:
- Let the initial mass of the block be M.
- Let the initial amplitude of the system be A.
- The spring constant is denoted as k.
2. Determine Initial Angular Frequency:
- The angular frequency ω of the system before the mass m is added can be calculated using the formula:
ω=√kM
3. Adding the Mass:
- When the mass m is added to the block, the total mass of the system becomes M+m.
4. Calculate New Angular Frequency:
- The new angular frequency ω′ after adding the mass can be calculated as:
ω′=√kM+m
5. Conservation of Momentum:
- At the moment the mass m is added, we can apply the conservation of momentum. Let v be the velocity of the block before adding the mass, and v′ be the velocity after adding the mass.
- The conservation of momentum gives us:
Mv=(M+m)v′
- Rearranging this, we find:
v′=MvM+m
6. Energy Conservation:
- The kinetic energy of the system before adding the mass is given by:
KEinitial=12Mv2
- The kinetic energy of the system after adding the mass is:
KEfinal=12(M+m)v′2
7. Relate Velocities and Amplitudes:
- The relationship between the velocities and amplitudes before and after can be expressed as:
vv′=√A2A′2
- Substituting v′ from the conservation of momentum into this equation allows us to express the new amplitude A′:
A′=A√MM+m
8. Final Results:
- The new amplitude of the system after adding the mass m is:
A′=A√MM+m
- The new angular frequency ω′ is:
ω′=√kM+m
Summary of Results:
- New Amplitude: A′=A√MM+m
- New Angular Frequency: ω′=√kM+m
- Let the initial mass of the block be M.
- Let the initial amplitude of the system be A.
- The spring constant is denoted as k.
- The angular frequency ω of the system before the mass m is added can be calculated using the formula:
ω=√kM
- When the mass m is added to the block, the total mass of the system becomes M+m.
- The new angular frequency ω′ after adding the mass can be calculated as:
ω′=√kM+m
- At the moment the mass m is added, we can apply the conservation of momentum. Let v be the velocity of the block before adding the mass, and v′ be the velocity after adding the mass.
- The conservation of momentum gives us:
Mv=(M+m)v′
- Rearranging this, we find:
v′=MvM+m
- The kinetic energy of the system before adding the mass is given by:
KEinitial=12Mv2
- The kinetic energy of the system after adding the mass is:
KEfinal=12(M+m)v′2
- The relationship between the velocities and amplitudes before and after can be expressed as:
vv′=√A2A′2
- Substituting v′ from the conservation of momentum into this equation allows us to express the new amplitude A′:
A′=A√MM+m
- The new amplitude of the system after adding the mass m is:
A′=A√MM+m
- The new angular frequency ω′ is:
ω′=√kM+m
- New Amplitude: A′=A√MM+m
- New Angular Frequency: ω′=√kM+m
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A horizontal spring -block system of mass 2kg executes S.H.M when the block is passing through its equilibrium position an object of mass 1kg is put on it the two move together The new amplitude of vibration is (A being its initial amplitude)
View SolutionA horizontal spring -block system of mass 2kg executes S.H.M when the block is passing through its equilibrium position an object of mass 1kg is put on it the two move together The new amplitude of vibration is (A being its initial amplitude)
View SolutionA horizontal spring is connedted to a mass M. It exectues simple harmonic motion. When the mass M passes through its mean position, an object of mass m is put on it ans the two move together. The ratio of frequencies before and after will be-
View SolutionA block of mass M attached to the free end of a spring of force constant k is nounted on a smooth horizontal table as shown in figure.
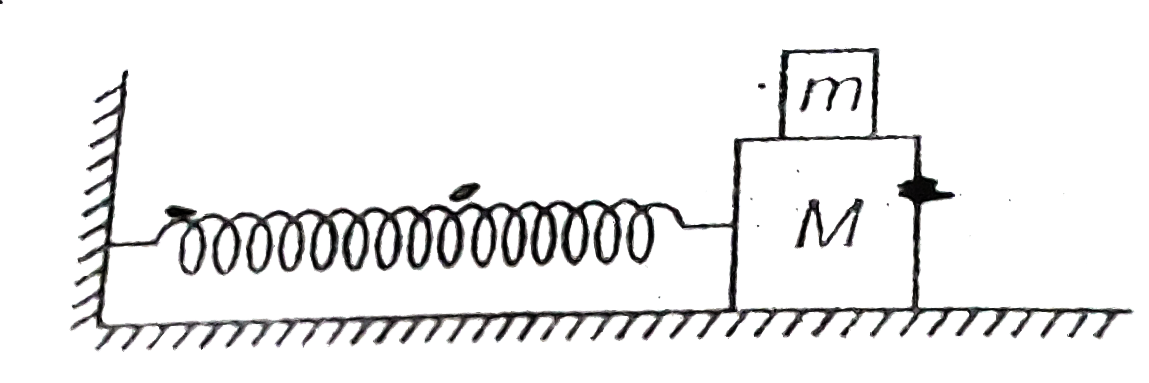
The block executes SHM with amplitude A and frequency f . If an object of mass m is put on it, when the block is passing through its equilibium position and the two move together ,then what is the new amplitude and frequency of vibration?
View SolutionA particle of mass 200g executes a simple harmonic motion. The restoring force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA paricle of mass 30kg executes a simple harmonic motion. The restorting force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA block with mass M attached to a horizontal spring with force constant k is moving with simple harmonic motion having amplitude A1. At the instant when the block passes through its equilibrium position a lump of putty with mass m is dropped vertically on the block from a very small height and sticks to it.
(a) Find the new amplitude and period.
(b) Repeat part (a) for the case in which the putty is dropped on the block when it is at one end of its path.
View SolutionA block with mass M attached to a horizontal spring with force constant k is moving with simple harmonic motion having amplitude A1. At the instant when the block passes through its equilibrium position a lump of putty with mass m is dropped vertically on the block from a very small height and sticks to it.
(a) Find the new amplitude and period.
(b) Repeat part (a) for the case in which the putty is dropped on the block when it is at one end of its path.
View SolutionThe system is in equilibrium and at rest. Now mass m1 is removed from m2. Find the time period and amplituded of resultant motion. Spring constant is K.

View SolutionA block of mass m moving at a speed v compresses a spring throgh a distance x before its speed is halved. Find the spring constant of the spring.
View Solution
