Question

A horizontal stretched string, fixed at two ends, is vibrating in its fifth harmonic according to the equation, ${\displaystyle t(x,t)=\left(0.01m\right)\sin \left[\left(62.8m^{-1}\right)t\right]}$. Assuming ${\displaystyle \pi =3.14}$, the correct statement ${\displaystyle \left(s\right)}$ is (are)

Options

A. (a) The number of nodes is `5`
B. (b) The length of the string is `0.25m`
C. ( c ) The maximum displacement of the midpoint of the string, from its equilibrium position is `0.01m`
D. (d) The fundamental frequency is `100 Hz`

Answer

B::C

Explanation

(b, c) `y = [0.01 sin(62.8x)] cos (628t)`.

`Length of string = 5 xx (1)/(20) = 0.25 m`
[ `because` `(2pi)/(lambda) = 62.8]`
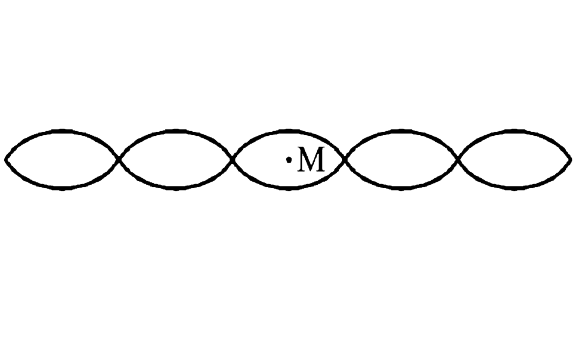
The midpoint `M` is an antitode and has the maximum displacement `= 0.01m`
`The fundamental frequency = (v)/(21) = (omeag//k)/(21) = 20 Hz`