(a) How is a toroid different from a solenoid?
(b) Show that in an ideal toroid, the magnetic field (i) inside the toroid and (ii) outside the toroid at any point in the open space is zero.
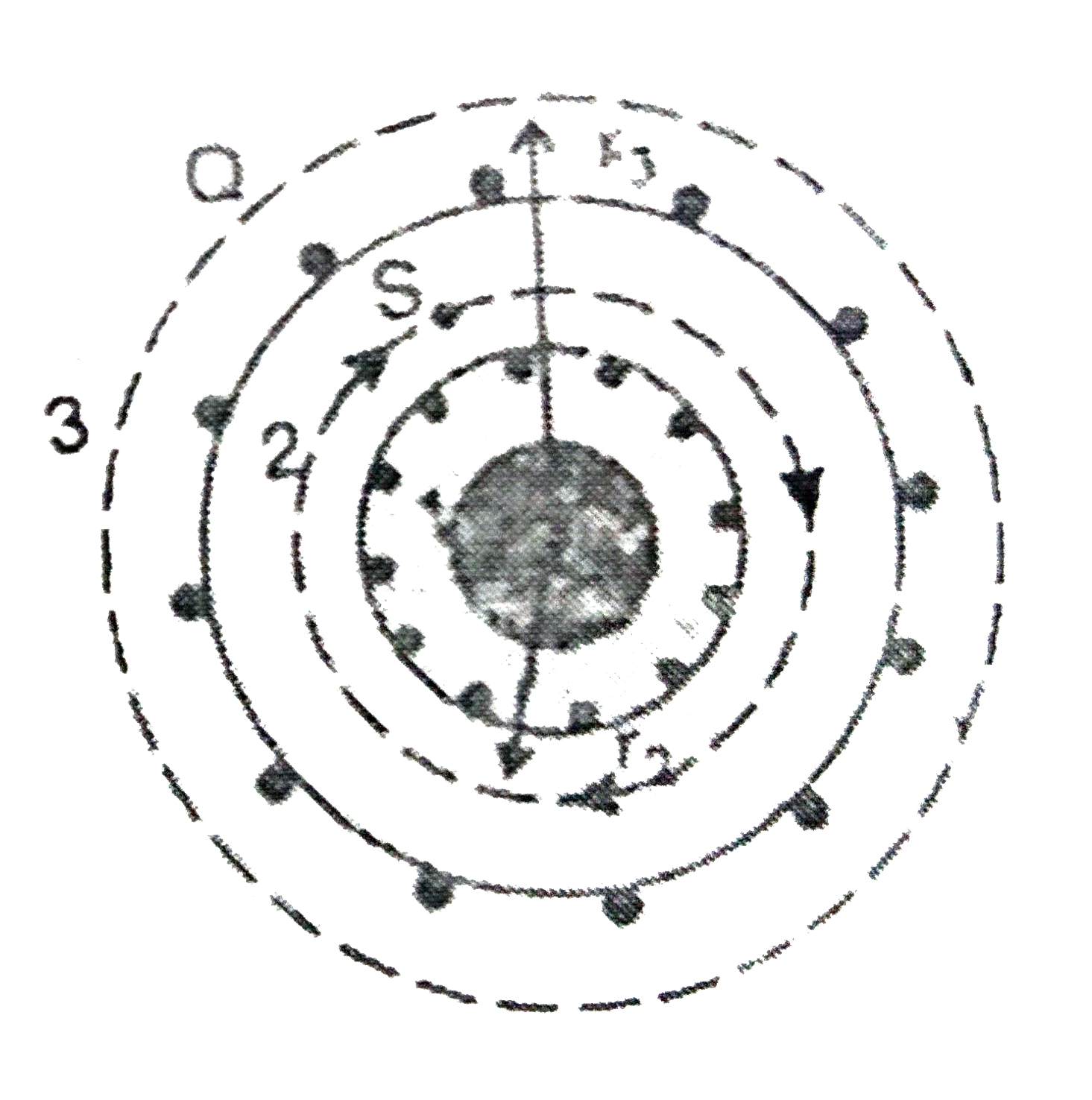
A toroid is essentially a solenoid which has been bent into a circular shape to close on itself.
(b) For the loop 1, Ampere's circuital law gives
B1.2πr1=μ0(0) i.e. B1=0
Thus, the magnetic field, in the open space inside the toroid is zero.
Also at point Q we have B3(2πr3)=μ0(I(enclosed))
But from the sectional cut, we see that the current coming out the plane of the paper is cancelled exactly by the current going into it.
Hence Ienclosed=0 ∴B3=0

Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - [SET - II DELHI BOARD]
6 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - [SET - III, DELHI BOARD]
6 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET - III (Delhi Board)
8 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Knowledge Check
Field inside a toroid is
Adirectly proportional to its lengthBdirectly proportional to currentCinversely proportional to total number of turnsDinversely proportional to currentThe magnetic induction due to toroidal solenoid is independent of
ApermeabilityBcurrentCradius of the toroidal solenoidDnumber of turns per unit length
Magnetic field induction at any point outside a toroid is ……………… .
View SolutionMagnetic Field Of A Toroid
View SolutionA toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are found. If the current in the wire is 11 A, what is the magnetic field (i) outside the toroid, (ii) inside the core of the toroid, and (iii) in the empty space surrounded by the toroid.
View SolutionA toroid has a core of inner radius 20cm and outer radius 22cm around which 4200 turns of a wire are wound. If the current in the wire is 10A, what is the magnetic field
(a) inside the core of toroid (b) outside the toroid
(c) in the empty space surrounded by toroid?
View Solution(a) Using Ampere's circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis.
(b) In what respect is a toroid different from a solenoid ? Draw and copare the patern of the magnetic field lines in the two cases.
(c) How is the magnetic field inside a given solenoid made strong?
View Solution(a)Using Ampere's circuital law,obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis.
(b)In what respect is a toroid different from a solenoid?Draw and compare the pattern of the magnetic field lines in the two cases.
(c)How is the magnetic field inside a given solenoid made strong?
View Solution
