(a) In a double-slit experiment, what ratio of d to a causes diffraction to eliminate the fourth bright side fringe? (b) what other bright fringes are also eliminated?
To solve the problem, we need to analyze the conditions under which diffraction causes the elimination of bright fringes in a double-slit experiment.
1. Understanding the Conditions for Minima and Maxima:
- In a double-slit experiment, the condition for minima (dark fringes) due to diffraction is given by:
dsinθ=mλ(1)
where m is an integer (order of the minimum), d is the distance between the slits, and λ is the wavelength of light.
- The condition for maxima (bright fringes) is given by:
dsinθ=nλ(2)
where n is an integer (order of the maximum).
2. Setting the Conditions for the 4th Bright Fringe:
- We want to eliminate the 4th bright fringe, which corresponds to n=4:
dsinθ=4λ(3)
3. Equating the Conditions for Minima and Maxima:
- For the 4th bright fringe to be eliminated, the condition for the 4th minimum must coincide with the condition for the 4th maximum. The first minimum occurs at m=1:
dsinθ=1λ(4)
- Setting equations (3) and (4) equal gives:
4λ=λa(5)
- Rearranging equation (5) leads to:
da=4
4. Conclusion for Part (a):
- The ratio of da that causes diffraction to eliminate the 4th bright fringe is:
da=4
Part (b): Finding Other Bright Fringes that are Eliminated
1. Identifying the Pattern of Eliminated Bright Fringes:
- From the analysis, we see that the condition for minima is m=1 for the first minimum. For higher orders of minima, the pattern continues as m=4k where k is an integer.
- Thus, the eliminated bright fringes will occur at:
n=4,8,12,…(6)
- This means every 4th bright fringe will be eliminated.
2. Conclusion for Part (b):
- The other bright fringes that are also eliminated are those corresponding to n=4k where k is any integer (i.e., 4th, 8th, 12th bright fringes, etc.).
Final Answers:
- (a) The ratio of da that eliminates the 4th bright fringe is 4.
- (b) The other bright fringes that are eliminated are the 4th, 8th, 12th, etc. bright fringes.
- In a double-slit experiment, the condition for minima (dark fringes) due to diffraction is given by:
dsinθ=mλ(1)
where m is an integer (order of the minimum), d is the distance between the slits, and λ is the wavelength of light.
- The condition for maxima (bright fringes) is given by:
dsinθ=nλ(2)
where n is an integer (order of the maximum).
- We want to eliminate the 4th bright fringe, which corresponds to n=4:
dsinθ=4λ(3)
- For the 4th bright fringe to be eliminated, the condition for the 4th minimum must coincide with the condition for the 4th maximum. The first minimum occurs at m=1:
dsinθ=1λ(4)
- Setting equations (3) and (4) equal gives:
4λ=λa(5)
- Rearranging equation (5) leads to:
da=4
- The ratio of da that causes diffraction to eliminate the 4th bright fringe is:
da=4
- From the analysis, we see that the condition for minima is m=1 for the first minimum. For higher orders of minima, the pattern continues as m=4k where k is an integer.
- Thus, the eliminated bright fringes will occur at:
n=4,8,12,…(6)
- This means every 4th bright fringe will be eliminated.
- The other bright fringes that are also eliminated are those corresponding to n=4k where k is any integer (i.e., 4th, 8th, 12th bright fringes, etc.).
- (a) The ratio of da that eliminates the 4th bright fringe is 4.
- (b) The other bright fringes that are eliminated are the 4th, 8th, 12th, etc. bright fringes.
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
66 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
23 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - CHECKPOINT
6 Videos
- HYDROGEN ATOMBOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)
6 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)
4 Videos
Similar Questions
Knowledge Check
In Young's double slit experiment the phase difference between the waves reaching the central fringe and fourth bright fringe will be
AzeroB4πC6πD8πIn the double-slit experiment, the distance of the second dark fringe from the central line are 3mm. The distance of the fourth bright fringe from the central line is
A6mmB8mmC12mmD16mmIn Young's double slit experiment a mica plate of refractive index μ is introduced in the path of light coming from one of the slit . If the central bright frige gets shifted to the point originally occupied by the fourth bright fringe, then the thickness of the mica plate will be ( symbols have their usual meaning )
A2λ(μ−1)B4λ3(μ−1)C4λ(μ−1)D2λ3(μ−1)
In a Young's double-slit experiment, the central bright fringe can be identified
View SolutionIn Young’s double slit experiment, the central bright fringe can be identified
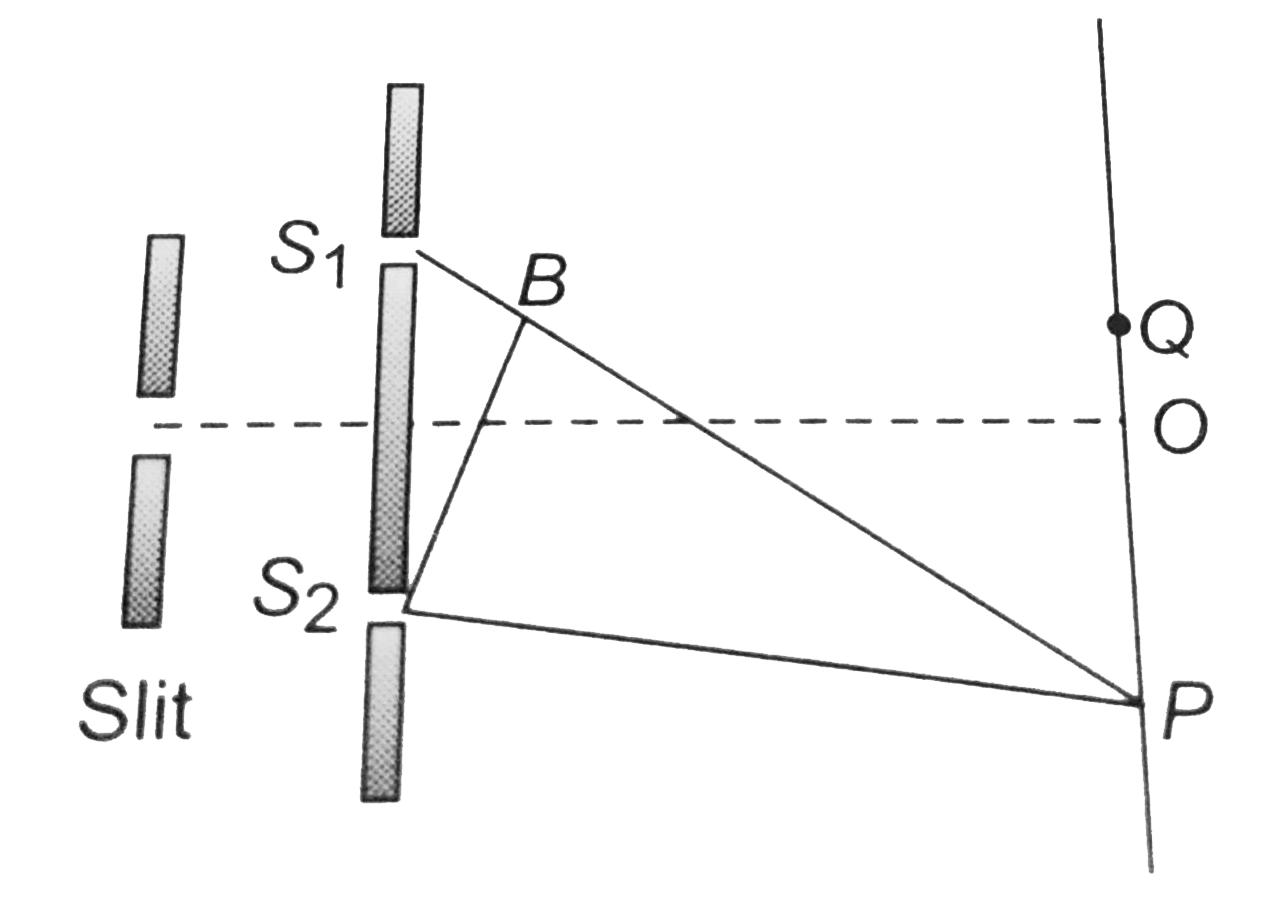
View SolutionIn the figure is shown Young's double slit experiment. Q is the position of the first bright fringe on the right side of O. P is the 11th bright fringe on the other side, as measured from Q. If the wavelength of the light used is 600nm. Then S1B will be equal to
View SolutionIn Young's double slit experiment, the phase difference between the light waves producing the third bright fringe from the central fringe will be (λ=6000 Å)
View SolutionIn the Young's double slit experiment, the interference pattern is found to have as intensity ratio between the bright and dark fringes as 9. This implies that
View Solution
