(a) In Fig. 32-19a, a beam of monochromatic light reflects and refracts at point A on the interface between material 1 with index of refraction $n_{1}$ = 1.33 and material 2 with index of refraction $n_{2} =$ 1.77. The incident beam makes an angle of $50^{\circ})$ with the interface. What is the angle of reflection at poinl A ? What is the angle of refraction there?

Text Solution

Verified by Experts

(1) The angle of reflection is equal to the angle of incidence, and both angles are measured relative to the normal to the surface at the point of reflection. (2) When light reaches the interface between two materials with different indexes of refraction ( call them $n_{1}$ and $n_{2}$ ), part of the light can be refracted by the interface according to Snell.s law, Eq. 33-35:
$n_{2} {sin θ}_{2} = n_{1} {sin θ}_{1}$
where both angles are measured relative to the normal at the point of refraction.
Calculations: In Fig. 32-19a, the normal at point A is drawn as a dashed line through the point. Note that the angle

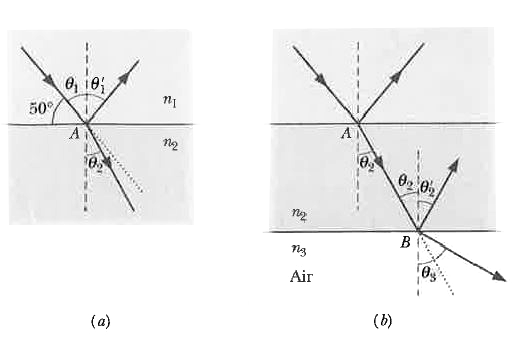
of incidence $θ$ , is not the given $50^{\circ}$ but is $90^{\circ} - 50^{\circ} = 40^{\circ}$ . Thus, the angle of reflection is
$θ_{1} = θ_{1} = 40^{\circ}$ .
The light that passes from material 1 into material 2 undergoes refraction at point A on the interface between the two materials. Again we measure angles between light rays and a normal, here at the point of refraction. Thus, in Fig. 32-19a, the angle of refraction is the angle marked $θ_{2}$ Solving Eq. 32-37 for $θ_{2}$ , gives us
$θ_{2} = {sin}^{- 1} (\frac{n_{1}}{n_{2}} {sin θ}_{1}) = {sin}^{- 1} (\frac{1.33}{1.77} {sin 40}^{\circ})$
$= {28.88}^{\circ} \approx 29^{\circ}$ .
This result means that the beam swings toward the normal (it was at $40^{\circ}$ to the normal and is now at $29^{\circ}$ .)
The reason is that when the light travels across the inter face, it moves into a material with a greater index of refraction. Caution: Note that the beam does not swing through the normal so that it appears on the left side of Fig. 32-194. (b) The light that enters material 2 at point A then reaches point B on the interface between material 2 and material 3, which is air, as shown in Fig. 32-19b. The interface through B is parallel to that through A. At B, some of the light reflects and the rest enters the air. What is the angle of reflection? What is the angle of refraction into the air?
Calculations: We first need to relate one of the angles at point B with a known angle at point A. Because the ntertace through point B IS parallel to that through point A, the incident angle at B must be equal to the angle of refraction $θ_{2}$ as shown in Fig. 32-19b. Then for reflection we again use the law of reflection. Thus, the angle of reflection at B is
$θ_{2} = θ_{2} = {28.88}^{\circ} \approx 29^{\circ}$ .
Next, the light that passes from material 2 into the air undergoes refraction at pointB, with refraction angle $θ_{3}$ Thus, we again apply Snell.s law of refraction, but this time we write Eq. 32-35 as
$n_{3} {sin θ}_{3} = n_{2} {sin θ}_{2}$ .
Solving for $θ_{3}$ then leads to
$θ_{3} = {sin}^{- 1} (\frac{n_{2}}{n_{3}} {sin θ}_{2}) = {sin}^{- 1} (\frac{1.77}{1.00} {sin 28.88}^{\circ})$
$= {58.75}^{\circ} \approx 59^{\circ}$ .
Thus, the beam swings away from the normal (it was at $29^{\circ}$ to the normal and is now at $59^{\circ}$ ) because it moves into a material (air) with a lower index of refraction

Updated on:21/07/2023