A jet of water with cross section of 6cm2 strikes a wall at an angle of 60∘ to the normal and rebounds elastically from the wall without losing energy. If the velocity of the water in the jet is 12m/s, the force acting on the wall is
0.864 N
86.4 N
72 N
7.2 N
The correct Answer is:B
To solve the problem step by step, we will follow these steps:
Step 1: Identify the given data
- Cross-sectional area of the jet, A=6cm2=6×10−4m2
- Velocity of the water jet, v=12m/s
- Angle of incidence with the normal, θ=60∘
Step 2: Calculate the components of the velocity
The velocity of the water jet can be broken down into two components:
- The component perpendicular to the wall (y-component):
vy=vsin(60∘)=12sin(60∘)=12×√32=6√3m/s
- The component parallel to the wall (x-component):
vx=vcos(60∘)=12cos(60∘)=12×12=6m/s
Step 3: Analyze the momentum change
Since the water jet rebounds elastically, the y-component of the velocity remains the same, while the x-component changes direction:
- Initial momentum in the x-direction: px,initial=mvx=m(6)
- Final momentum in the x-direction (after rebounding): px,final=m(−vx)=m(−6)
The change in momentum in the x-direction is:
Δpx=px,final−px,initial=m(−6)−m(6)=−12m
Step 4: Calculate the mass flow rate
The mass flow rate (˙m) of the water jet can be calculated using the formula:
˙m=ρAv
Where:
- ρ (density of water) = 1000kg/m3
- A=6×10−4m2
- v=12m/s
Substituting the values:
˙m=1000×(6×10−4)×12=7.2kg/s
Step 5: Calculate the force acting on the wall
The force (F) acting on the wall is given by the rate of change of momentum:
F=ΔpxΔt=˙m⋅Δvx
Where Δvx=12m/s (since the change in momentum is 12m for each second).
Thus:
F=˙m⋅12=7.2⋅12=86.4N
Final Answer
The force acting on the wall is 86.4N.
---
- Cross-sectional area of the jet, A=6cm2=6×10−4m2
- Velocity of the water jet, v=12m/s
- Angle of incidence with the normal, θ=60∘
The velocity of the water jet can be broken down into two components:
- The component perpendicular to the wall (y-component):
vy=vsin(60∘)=12sin(60∘)=12×√32=6√3m/s
- The component parallel to the wall (x-component):
vx=vcos(60∘)=12cos(60∘)=12×12=6m/s
Since the water jet rebounds elastically, the y-component of the velocity remains the same, while the x-component changes direction:
- Initial momentum in the x-direction: px,initial=mvx=m(6)
- Final momentum in the x-direction (after rebounding): px,final=m(−vx)=m(−6)
Δpx=px,final−px,initial=m(−6)−m(6)=−12m
The mass flow rate (˙m) of the water jet can be calculated using the formula:
˙m=ρAv
Where:
- ρ (density of water) = 1000kg/m3
- A=6×10−4m2
- v=12m/s
˙m=1000×(6×10−4)×12=7.2kg/s
The force (F) acting on the wall is given by the rate of change of momentum:
F=ΔpxΔt=˙m⋅Δvx
Where Δvx=12m/s (since the change in momentum is 12m for each second).
F=˙m⋅12=7.2⋅12=86.4N
The force acting on the wall is 86.4N.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
A jet water, whose cross section is A strikes a wall making an angle θ with normal and elastically rebounds. The velocity of water of density ρ is v. Force exerted on wall is :-
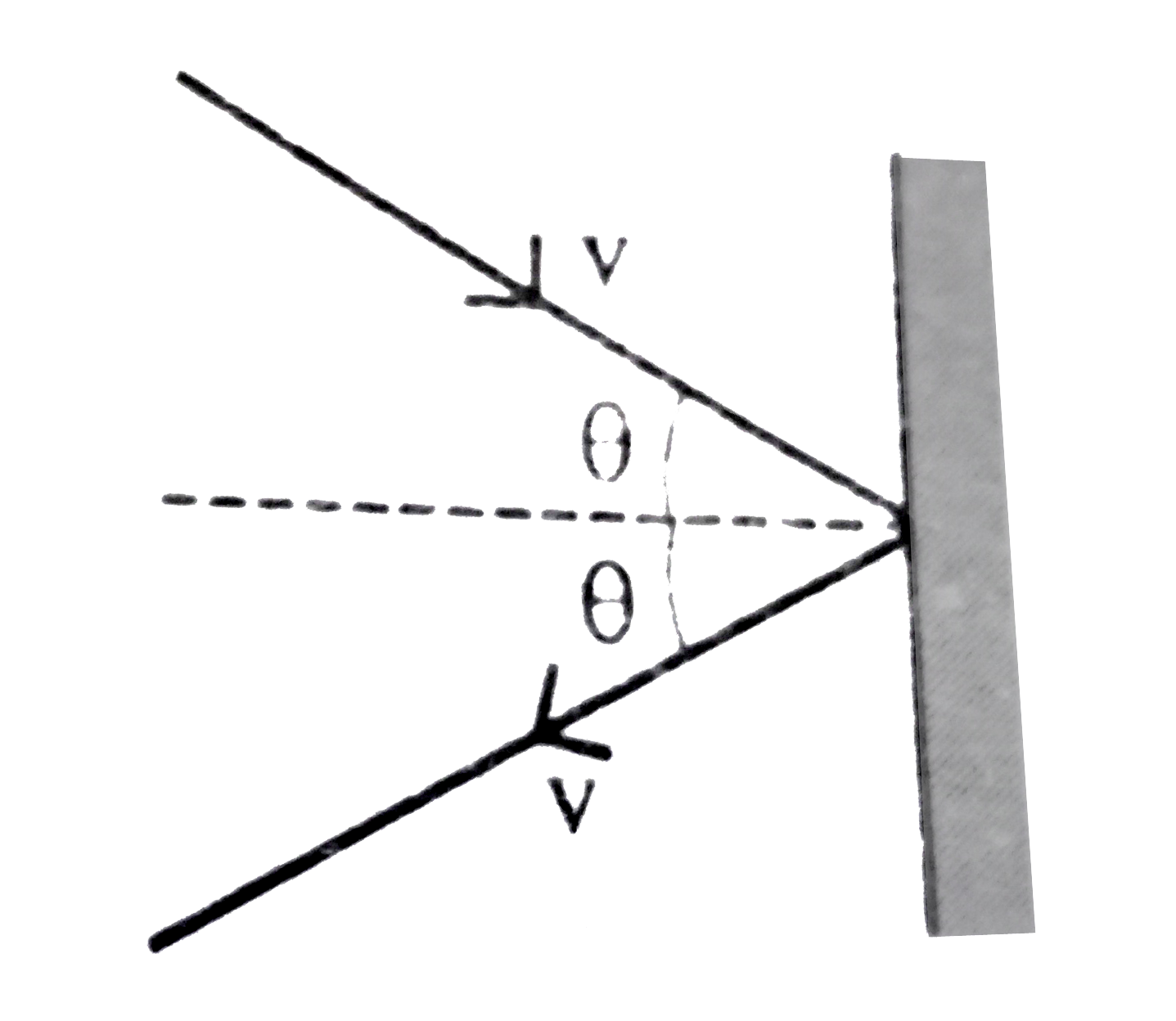
View SolutionA 0.5kg ball moving with a speed of 12m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle . If the ball is in contact with the wall for 0.25s, the average force acting on the wall is

View SolutionWater from a hosepipe of radius 5 cm strikes a wall at a speed of 5ms−1 normally and stops. The force exerted on the wall in newton is
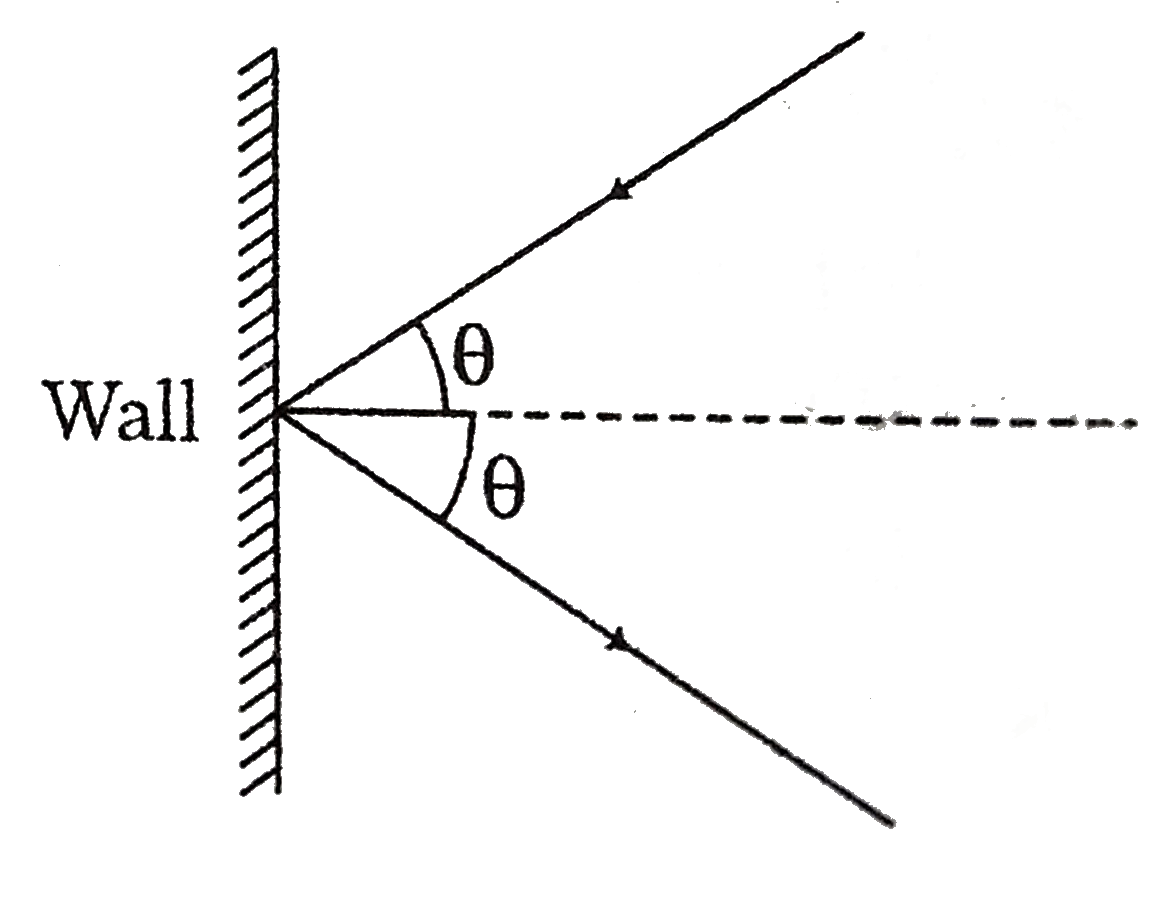
View SolutionThe mass of hydrogen molecule is 3.32×10−27 kg. If 1023 hydrogen molecules strikes per second at 2 cm2 area of a rigid wall at an angle of 45∘ from the normal and rebound back with a speed of 1000 ms−1, then the pressure exerted on the wall is
View SolutionAn object of m kg with speed of v ms−1 strikes a wall at an angle θ and rebounds at the same speed and same angle. Find the magnitude of change in the momentum of object.
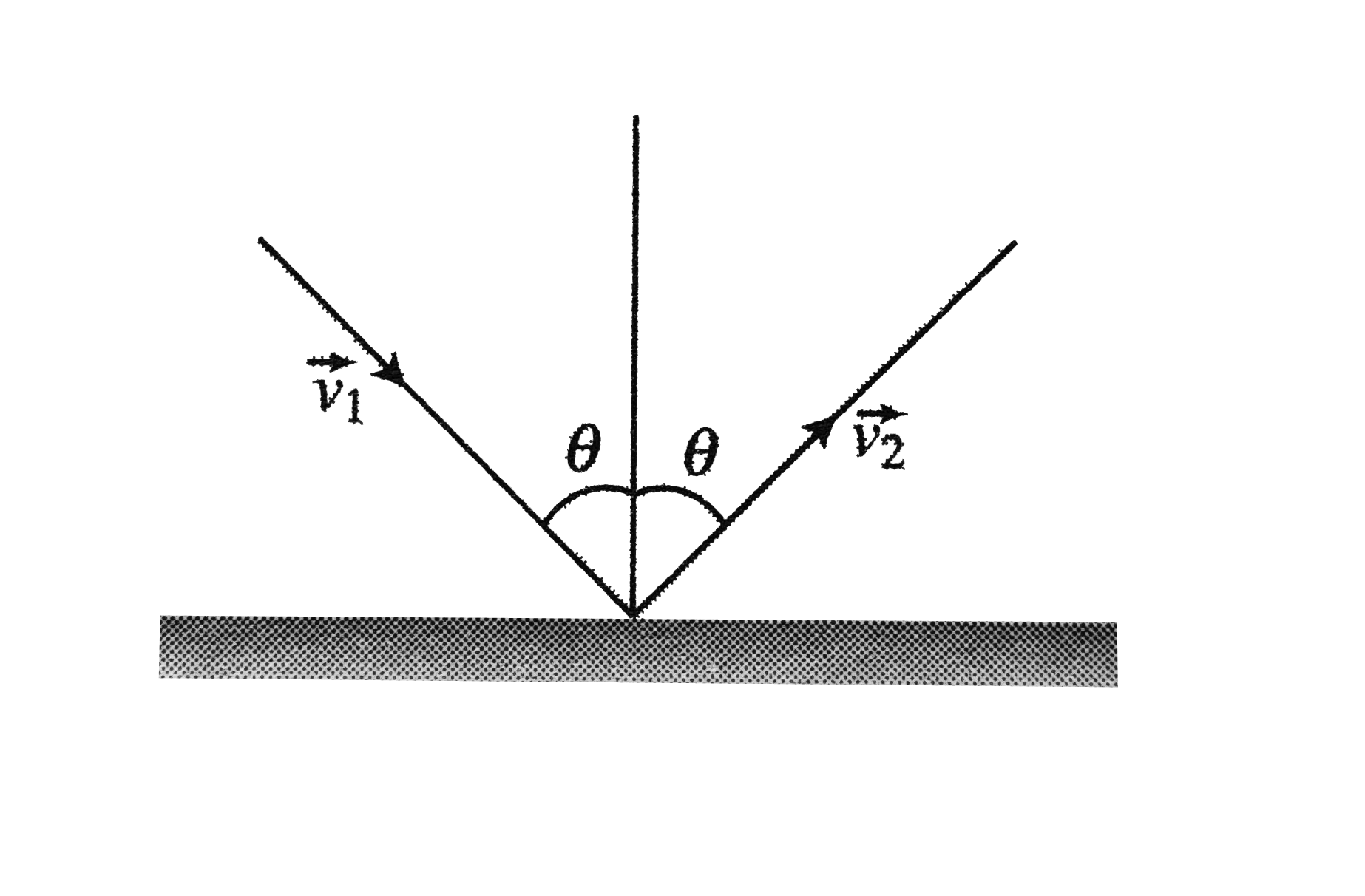
View SolutionAn object of m kg with speed of v ms−1 strikes a wall at an angle θ and rebounds at the same speed and same angle. Find the magnitude of change in the momentum of object.

View SolutionA 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60o with the wall and reflects at the same angle. If it remains in contact with the wall for 0.1 s, then the force is
View SolutionA ball of mass 3kg moving with a speed of 100 m/s, strikes a wall at an angle 60∘ (as shown in figure). The ball rebounds at the same speed and remains in contact with the wall for 0.2 s, the force exerted by the ball on the wall is

View SolutionA horizontal jet of water coming out of a pipe of area of cross - section 20 cm2 hits a vertical wall with a velocity of 10 ms−1 and rebounds with the same speed. The force exerted by water on the wall is,
View SolutionA particle of mass m strikes elastically on a wall with velocity v, at an angle of 60∘ from the wall then magnitude of change in momentum of ball along the wall is
View Solution
