A 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60o with the wall and reflects at the same angle. If it remains in contact with the wall for 0.1 s, then the force is
Zero
40√3N
10√3N
5√3N
To solve the problem step by step, we will analyze the motion of the particle before and after it strikes the wall, calculate the change in momentum, and then use that to find the force exerted by the wall on the particle.
Step 1: Understand the Problem
A particle of mass m=1kg strikes a wall with a velocity of v=1m/s at an angle of 60∘ with the wall. It reflects off the wall at the same angle and remains in contact with the wall for t=0.1s.
Step 2: Break Down the Velocity into Components
The velocity of the particle can be broken down into horizontal and vertical components:
- Horizontal component before collision:
vx=vcos(60∘)=1⋅cos(60∘)=1⋅12=0.5m/s
- Vertical component before collision:
vy=vsin(60∘)=1⋅sin(60∘)=1⋅√32=√32m/s
Step 3: Determine the Momentum Before and After Collision
The momentum before the collision can be calculated as:
- Initial momentum in the horizontal direction:
px,initial=mvx=1⋅0.5=0.5kg m/s
- Initial momentum in the vertical direction:
py,initial=mvy=1⋅√32=√32kg m/s
After the collision, the horizontal component remains the same, but the vertical component changes direction:
- Final momentum in the horizontal direction:
px,final=mvx=1⋅0.5=0.5kg m/s
- Final momentum in the vertical direction (upward):
py,final=−mvy=−1⋅√32=−√32kg m/s
Step 4: Calculate the Change in Momentum
The change in vertical momentum (Δpy) is:
Δpy=py,final−py,initial=−√32−√32=−√3kg m/s
Step 5: Calculate the Average Force
The average force exerted by the wall can be calculated using the formula:
F=ΔpΔt
Substituting the values:
F=−√30.1=−10√3N
Since we are interested in the magnitude of the force, we take the positive value:
F=10√3N
Final Answer
The force exerted by the wall on the particle is 10√3N.
---
A particle of mass m=1kg strikes a wall with a velocity of v=1m/s at an angle of 60∘ with the wall. It reflects off the wall at the same angle and remains in contact with the wall for t=0.1s.
The velocity of the particle can be broken down into horizontal and vertical components:
- Horizontal component before collision:
vx=vcos(60∘)=1⋅cos(60∘)=1⋅12=0.5m/s
- Vertical component before collision:
vy=vsin(60∘)=1⋅sin(60∘)=1⋅√32=√32m/s
The momentum before the collision can be calculated as:
- Initial momentum in the horizontal direction:
px,initial=mvx=1⋅0.5=0.5kg m/s
- Initial momentum in the vertical direction:
py,initial=mvy=1⋅√32=√32kg m/s
- Final momentum in the horizontal direction:
px,final=mvx=1⋅0.5=0.5kg m/s
- Final momentum in the vertical direction (upward):
py,final=−mvy=−1⋅√32=−√32kg m/s
The change in vertical momentum (Δpy) is:
Δpy=py,final−py,initial=−√32−√32=−√3kg m/s
The average force exerted by the wall can be calculated using the formula:
F=ΔpΔt
Substituting the values:
F=−√30.1=−10√3N
Since we are interested in the magnitude of the force, we take the positive value:
F=10√3N
The force exerted by the wall on the particle is 10√3N.
Similar Questions
A 0.5kg ball moving with a speed of 12m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle . If the ball is in contact with the wall for 0.25s, the average force acting on the wall is

View SolutionA 3.00kg steel hall strikes the wall with a speed of 10.0m/s at an angle of 60∘ with the surface. It bounces off with the same speed and angle. If the ball is in contact with the wall for 0.200s, what is the average force exerted by the wall on the ball?
View Solution
Knowledge Check
A 3 kg ball strikes a heavy rigid wall with a speed of 10 m/s at an angle of 60∘. It gets reflected with the same speed and angle as shown in Fig. 15.3.11. It the ball is in contact with the wal for 0.20 s, what is the average force exerted on the ball by the wall ?
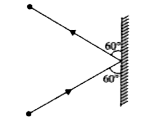 AzeroB150 NC150 √3 ND300 N
AzeroB150 NC150 √3 ND300 N
A ball of mass 600 gm strikes a wall with a velocity of 5ms−1 at an angle 30∘ with the wall and rebounds with the same speed at the same angle with the wall. The change in momentum of the ball is, (in kg ms−1)
View SolutionA ball of mass 3kg moving with a speed of 100 m/s, strikes a wall at an angle 60∘ (as shown in figure). The ball rebounds at the same speed and remains in contact with the wall for 0.2 s, the force exerted by the ball on the wall is

View SolutionA ball strikes a wall with a velocity →u at an angle θ with the normal to the wall surface. and rebounds from it at an angle β with the surface. Then
View SolutionA particle of mass m strikes elastically on a wall with velocity v, at an angle of 60∘ from the wall then magnitude of change in momentum of ball along the wall is
View SolutionA 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
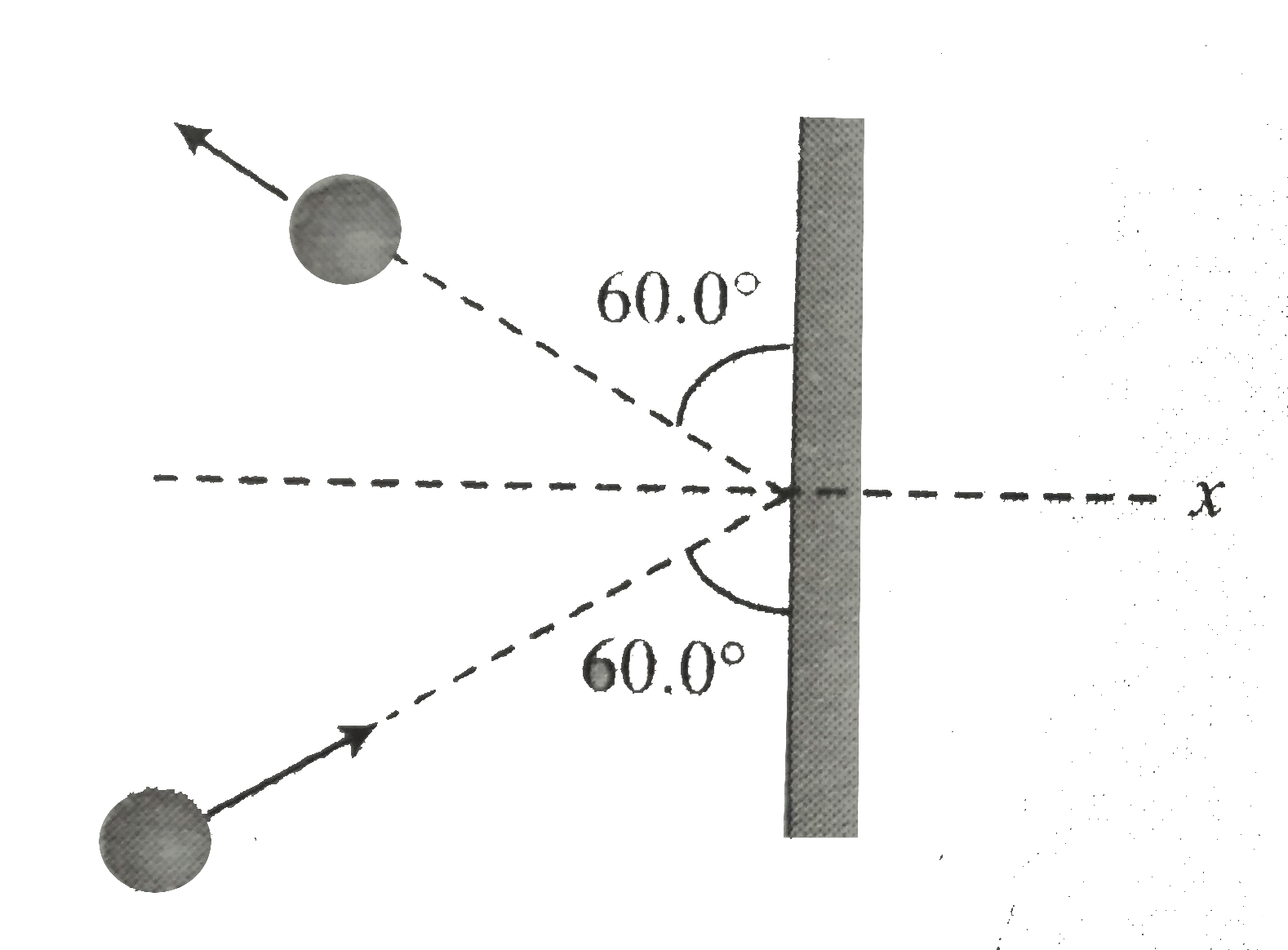
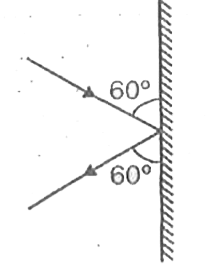
View SolutionA body of mass 3 kg moving with velocity 10 m/s hits a wall at an angle of 60∘ and returns at the same angle. The impact time was 0.2 s. Calculate the force exerted on the wall.
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
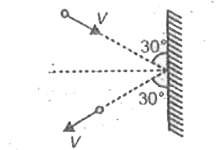
View Solution