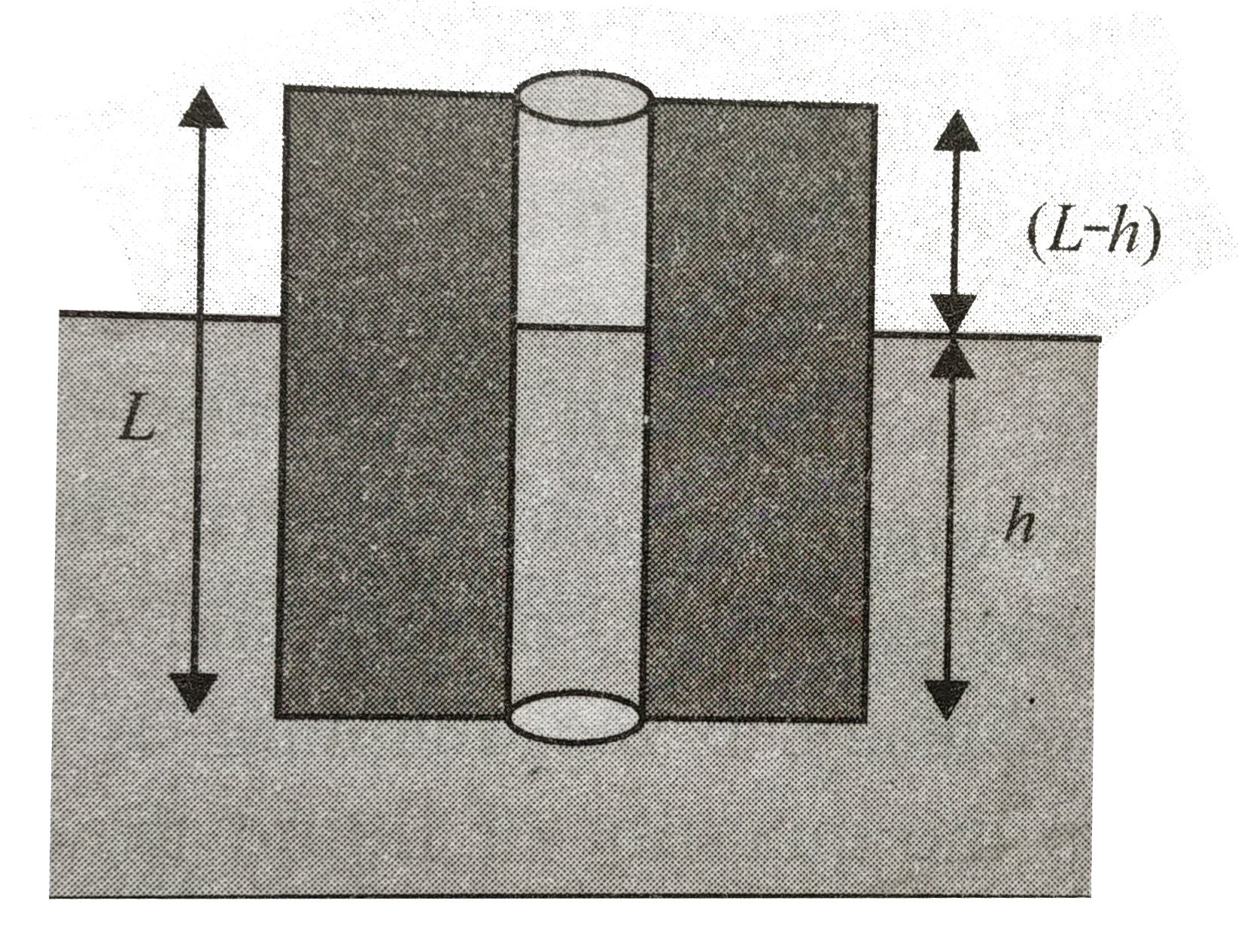
A large block of ice cuboid of edge length 'l' and density ρice−0.9ρw, has a larger vertical hole along its axis. This block is floating in a lake. Find out length of the rope required to raise a bucket of water through the hole.
l/2
l/4
l/8
l/10
The correct Answer is:D
Step by step video, text & image solution for A large block of ice cuboid of edge length 'l' and density rho_(ice) -0.9 rho_(w), has a larger vertical hole along its axis. This block is floating in a lake. Find out length of the rope required to raise a bucket of water through the hole. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - Advanced MCQ with one or more options correct
18 Videos
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - Unsolved Numerical Problems
86 Videos
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - MCQ
17 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical
94 Videos
Similar Questions
A large block of ice cuboid of height 'l' and density ρice=0.9ρw' has a large vertical hole along its axis. This block is floating in a lake. Find out the length of the rope required to raise a bucket of water through the hole.
View SolutionA large block of ice 10 cm thick with a vertical hole drilled through it is floating in a lake. The minimum length of the rope required to scoop out a bucket full of water through the hole is (0.2x)m. Find the value of x. Take density of ice =0.9 g/cm3
View Solution
Knowledge Check
A large block of ice 4 m thick has a vertical hole drilled through it and is floating in the middle of water in a lake. The minimum length of rope required to scoop up a bucket full of the through the hole is (density of ice =0.9CGS unit, density of water =1CGS unit)
A40 cmB24 cmC20 cmD360 cmThe thickness of the ice layer on the surface of lake is 20 m. A hole is made in the ice layer. What is the minimum length of the rope required to take a bucket full of water out ? (Take density of ice =0.9×103kg/m3)
A2 mB5 mC9 mD18 mA large block of ice 10 cm thick with a vertical hole drilled through it is floating in a lake. The minimum of water through the hole is (density of ice =0.9gcm−3)
A0.5 mB1.0 mC1.2 mD1.8 m
A large block of ice 5m thick has a vertical hole drilled through it and is floating in the middle of a lake. What is the minimum length of a rope required to scoop up a bucket full of water through the hole? Relative density of ice =0.9.
View SolutionIn the middle of a pond, a large ice block of 10 m thickness of floating. Let a vertical hole is drilled in this block. The minimum length (in cm) of a rope required to lift a bucket full of water through the hole is x×10cm? (Specify gravity of ice =0.91).
View SolutionA block of ice with an area A and a height h floats in water of density ρ0. What work should be performed to submerge the ice block completely into water if density of ice is ρ1 ?
View Solution(i) A cylindrical container has area of cross section equal to 4A and it contains a non viscous liquid of density 2ρ. A wooden cylinder of cross sectional area A and length L has density ρ. It is held vertically with its lower surface touching the liquid. It is released from this position. Assume that the depth of the container is sufficient and the cylinder does not touch the bottom.
(a) Find amplitude of oscillation of the wooden cylinder.
(b) Find time period of its oscillation.
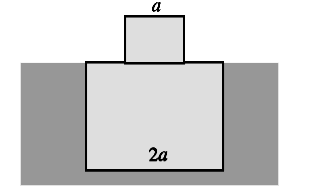
Two cubical blocks of side length a and 2a are stuck symmetrically as shown in the figure. The combined block is floating in water with the bigger block just submerged completely. The block is pushed down a little and released. Find the time period of its oscillation. Neglect viscostiy.
View SolutionA very large block of ice of the size of a volleyball court and of uniform thickness of 8m is floating on water. A person standing near its edge wishes to fetch a bucketful of water using a rope. The smallest length of rope required for this is about
View Solution
