A large container has a sliding vertical wall of height H so as to divide it into two parts. The partition wall is connected to the left container wall by an ideal spring of force constant k. when the spring is relaxed the dimentsions of the floor of the right part is Lxxb. Now water (density ρ) is slowly poured into the right chamber. what is the maximum volume of water that can be stored in the right chamber without spilling it into the other part. The partition wall slides without friction.

The correct Answer is:Hb(L+ρgbH22K)
Step by step video, text & image solution for A large container has a sliding vertical wall of height H so as to divide it into two parts. The partition wall is connected to the left container wall by an ideal spring of force constant k. when the spring is relaxed the dimentsions of the floor of the right part is Lxxb. Now water (density rho) is slowly poured into the right chamber. what is the maximum volume of water that can be stored in the right chamber without spilling it into the other part. The partition wall slides without friction. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
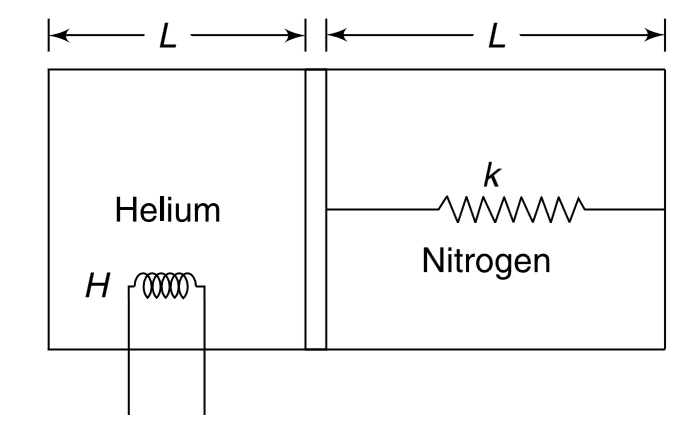
An adiabatic cylinder has length 2 L and cross sectional area A. A freely moving non conducting piston of negligible thickness divides the cylinder into two equal parts. The piston is connected to the right face of the cylinder with an ideal spring of force constant k. The right chamber contains 28 g nitrogen in which one third of the molecules are dissociated into atoms. The left chamber container 4 g helium. With piston in equilibrium and spring relaxed the pressure in both chamber is P0. The helium chamber is slowly given heat using an electric heater (H), till the piston moves to right by a distance 3L4. Neglect the volume occupied by the spring and the heating coil. Also neglect heat capacity of the spring.
(a) Find the ratio of CP and CV for nitrogen gas in right chamber.
(b) Calculate change in temperature of helium.
(c) Calculate heat supplied by the heater.
View SolutionWhat will be the spring constant k of a spring if spring is divided in n equal parts?
View Solution
Knowledge Check
If a spring of force constant k is divided into n equal parts , then force constant of each part is
AkBknCno force will actDnkAn ideal spring of force constant k is broken into two identical pieces. The force constant of each of the smaller springs is :
Ak/2BkC2kD4kAn ideal spring of force constant k is broken into two identical pieces. The force constant of each of the smaller springs is :
Ak/2BkC2kD4k
If a spring of force constant 'k' is cut into two parts, such that one part is thrice in length of the other part. Then the force constant of each part are
View SolutionA spring of force constant k is cut into there equal part what is force constant of each part ?
View SolutionA spring obeying Hooke's law has a force constant k. Now if the spring is cut in two equal parts, the force constant of each part is:
View SolutionA square field of 2sq. Km is to be divided into two equal parts by a wall which coincides with a diagonal. Find the length of the wall :
View SolutionA square field of 2sq. Km is to be divided into two equal parts by a wall which coincides with a diagonal. Find the length of the wall :
View Solution
