A large force is acting on a body for a short time. The impulse imparted is equal to the change in
1.acceleration
2.momentum
3. energy
4. velocity
The correct Answer is:B
To solve the question, we need to understand the relationship between impulse and momentum. Here’s a step-by-step breakdown:
Step 1: Understand Impulse
Impulse (I) is defined as the product of the average force (F) acting on an object and the time duration (Δt) for which the force acts. Mathematically, it can be expressed as:
I=F⋅Δt
Step 2: Relate Impulse to Momentum
According to Newton's second law, the force acting on an object is equal to the rate of change of momentum (p) of that object. This can be expressed as:
F=ΔpΔt
where Δp is the change in momentum.
Step 3: Rearranging the Equation
From the equation in Step 2, we can rearrange it to find the change in momentum:
Δp=F⋅Δt
Step 4: Connect Impulse and Change in Momentum
From Step 1 and Step 3, we see that:
I=F⋅Δt=Δp
This shows that the impulse imparted to the body is equal to the change in momentum of the body.
Conclusion
Therefore, the impulse imparted is equal to the change in momentum.
Final Answer
The impulse imparted is equal to the change in momentum.
---
Impulse (I) is defined as the product of the average force (F) acting on an object and the time duration (Δt) for which the force acts. Mathematically, it can be expressed as:
I=F⋅Δt
According to Newton's second law, the force acting on an object is equal to the rate of change of momentum (p) of that object. This can be expressed as:
F=ΔpΔt
where Δp is the change in momentum.
From the equation in Step 2, we can rearrange it to find the change in momentum:
Δp=F⋅Δt
From Step 1 and Step 3, we see that:
I=F⋅Δt=Δp
This shows that the impulse imparted to the body is equal to the change in momentum of the body.
Therefore, the impulse imparted is equal to the change in momentum.
The impulse imparted is equal to the change in momentum.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - HOTS
8 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Exemplar Problems
9 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar
5 Videos
Similar Questions
Knowledge Check
A force of 50 N acts on a body for 10 s. What will be the change in momentum of the body ?
A200 N.sB400 N.sC500 N.sD1000 N.s
Four forces are acting on a body as shown in figure. The magnitude of resultant of the forces is
View SolutionA force F is acted on a body as shown in the figure. Find the impulse of the force in first four seconds.

View SolutionA force of 5 N acts on a body for 2 milliseconds. Calculate the impulse. If the mass of the body is 5 g, calculate the change of velocity.
View SolutionAssertion : Impulsive force is large are acts for a short time.
Reason : Finite change in momentum should be produced by the force.
View SolutionThe following problems illustrate the effect of a time-dependent force of a large average magnitude which acts on a moving object only for a short duration. Such forces are called 'impulsive' forces. According to the impulse-momentum theorem, impulse delivered to a body is equal to the change of linear momentum of the body.
A ball of mass 250g is thrown with a speed of 30m/s. The ball strikes a bat and it is hit straight back along the same line at a speed of 50m/s. Variation of the interaction force, as long as the ball remains in contact with the bat, is as shown in Fig.
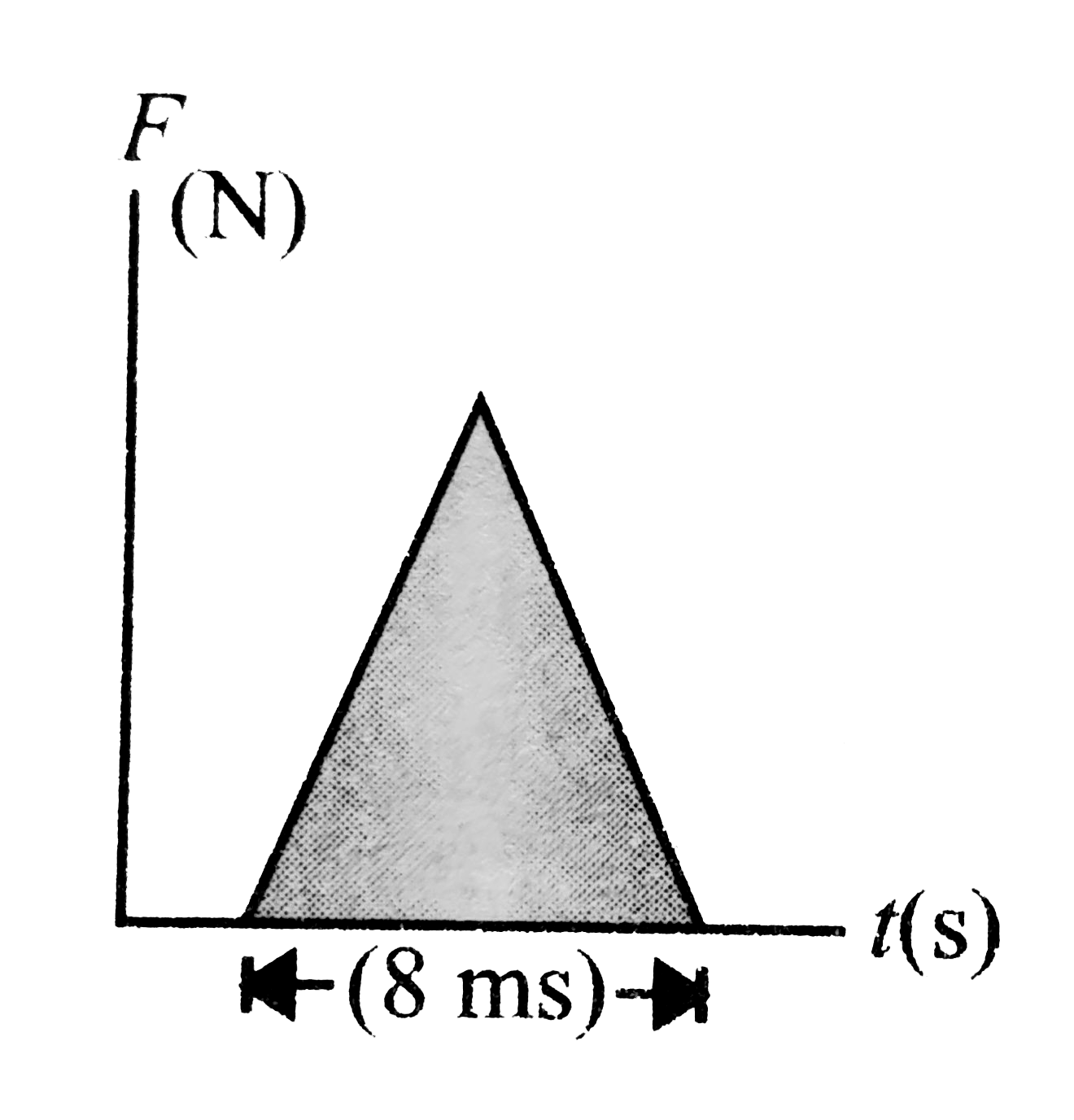
Maximum force exerted by the bat on the ball is
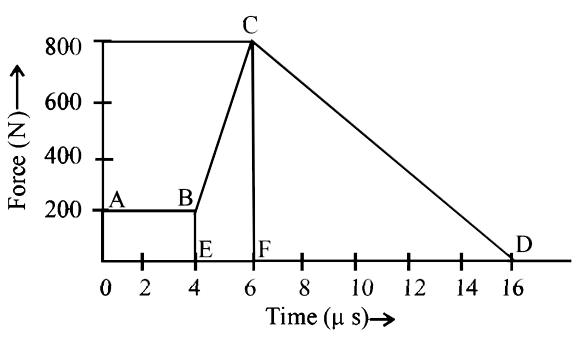
View SolutionThe magnitude of the force (in newtons) acting on a body varies with time t (in micro seconds) as shown in the fig AB, BC and CD are straight line segments. The magnitude of the total impulse of the force on the body from t=4μs to t=16μs is ….Ns
View SolutionTwo force F1 and F2 are acting on a body. One force is double that of the other force and the resultant is equal to the greater force. Then the angle between the two forces is :-
View Solution
