A laser beam of 7,500Å is sent from a lunar rover on the moon. If laser beam passes through an aperture of 0.8 cm, calculate the angular spread of diffracted beam on reaching the Earth. The distance between the Earth and the moon is 4×105km.
The correct Answer is:18.75×10−5 radian
To solve the problem of calculating the angular spread of a diffracted beam from a laser sent from the moon to the Earth, we can follow these steps:
Step 1: Identify the Given Values
- Wavelength of the laser beam, λ=7500Å=7500×10−10m=7.5×10−7m
- Aperture diameter, b=0.8cm=0.8×10−2m
- Distance from the moon to the Earth is not directly needed for calculating the angular spread.
Step 2: Use the Formula for Angular Spread
The angular spread θ for a single slit diffraction can be approximated using the formula:
θ≈λb
where λ is the wavelength and b is the width of the aperture.
Step 3: Substitute the Values into the Formula
Substituting the values of λ and b:
θ≈7.5×10−70.8×10−2
Step 4: Calculate θ
Calculating the above expression:
θ≈7.5×10−70.8×10−2=7.50.8×10−5=9.375×10−5radians
Step 5: Calculate the Angular Spread
The total angular spread is given by 2θ:
Angular Spread=2θ=2×9.375×10−5=1.875×10−4radians
Final Answer
Thus, the angular spread of the diffracted beam on reaching the Earth is:
Angular Spread≈1.875×10−4radians
---
- Wavelength of the laser beam, λ=7500Å=7500×10−10m=7.5×10−7m
- Aperture diameter, b=0.8cm=0.8×10−2m
- Distance from the moon to the Earth is not directly needed for calculating the angular spread.
The angular spread θ for a single slit diffraction can be approximated using the formula:
θ≈λb
where λ is the wavelength and b is the width of the aperture.
Substituting the values of λ and b:
θ≈7.5×10−70.8×10−2
Calculating the above expression:
θ≈7.5×10−70.8×10−2=7.50.8×10−5=9.375×10−5radians
The total angular spread is given by 2θ:
Angular Spread=2θ=2×9.375×10−5=1.875×10−4radians
Thus, the angular spread of the diffracted beam on reaching the Earth is:
Angular Spread≈1.875×10−4radians
Topper's Solved these Questions
- WAVE OPTICALBOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - PRACTICE PROBLEMS (3)
10 Videos
- WAVE OPTICALBOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - PRACTICE PROBLEMS (4)
9 Videos
- WAVE OPTICALBOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - PRACTICE PROBLEMS (1)
23 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
Determine the diameter of the image formed by a spherical concave mirror of focal length 8 m. The diameter of the moon is 3450 km and the distance between the earth and the moon is approx 4×105 km.
View SolutionFind the diameter of the image of the moon formed by a spherical concave mirror of focal length 7.6 m. The diameter of the moon is 3450 km and the distance of the earth and the moon is 3.8×105km.
View Solution
Knowledge Check
A bomb explodes on moon. How long does the sound take to reach the earth coverage distance between earth and moon is 3.8×108m?
A1.16×106sB10sC1.16×106hDsound is not transmitted to earthA laser beam having λ=7000 Å and aperture d=10−2m is sent to the moon. What is the angular spread of the beam?
A7×10−4 radianB(7×10−4×10π180)0C7×10−5 radianD72×10−5 radianLight from a laser (λ=640nm) passes through a diffraction grating and spreads out into three beams as shown in the figure. Determine the spacing between the slits of the grating
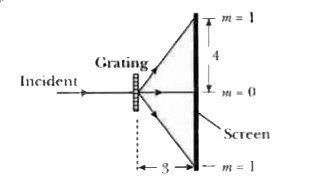 A240 nmB680 nmC410 nmD800 nm
A240 nmB680 nmC410 nmD800 nm
Find the distance of a point from the earth's centre where the resultant gravitational field due to the earth and the moon is zero. The mass of the earth is 6.0×1024 kg and that of the moon is 7.4x1022 kg. The distance between the earth and the moon is 4.0×105km.
View SolutionA laser beam has a wavelength of 6×10−7m and aperture of 6×10−2m. The beam is sent towards the moon which is at a distance of 4×108m from the earth. Calculate (i) angular spread of the beam and (ii) the arel spread when it reaches the moon.
View SolutionFind the distance of a point from the earth's centre where the resultant gravitational field due to the earth and the moon is zero The mass of the earth is 6.0×1024kg and that of the moon is 7.4×1022kg The distance between the earth and the moon is 4.0×105km .
View SolutionFind the distance of a point from the earth's centre where the resultant gravitational field due to the earth and the moon is zero. The mass of the earth is 6.0×1024kg and that of the moon is 7.4×1022kg. The distance between the earth and the moon is 4.0×105km.
View SolutionA parallel beam of light of wavelength 4000Å passes through a slit of width 5×10−3m. The angular spread of the central maxima in the diffraction pattern is
View Solution
