A lens forms an upright and diminished image of an object when the object is placed at the focal point of the given lens.
Name the lens.
Convave lens.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A virtual, diminished image is formed when an object is placed between the optical centre and the principal focus of a lens.
Name the type of lens which forms the above image.AconvexBconcaveCbothDnone
A lens forms a virtual, diminished image of an object placed at 2m from it. The size of image is half of the object. Which one of the following statements is correct regarding the nature and focal length of the lens?
View SolutionA convex lens is used to obtain a magnified image of an object on a screen . The object is at a distance 10 m from the lens . If the magnification is 19. the focal length of the lens is
View SolutionA lens forms a real image of an object. The distance from the object to the lens is x cm and that from the lens to the image is y cm. The graph shows the variation of y with x.
It can be deduced that the lens is
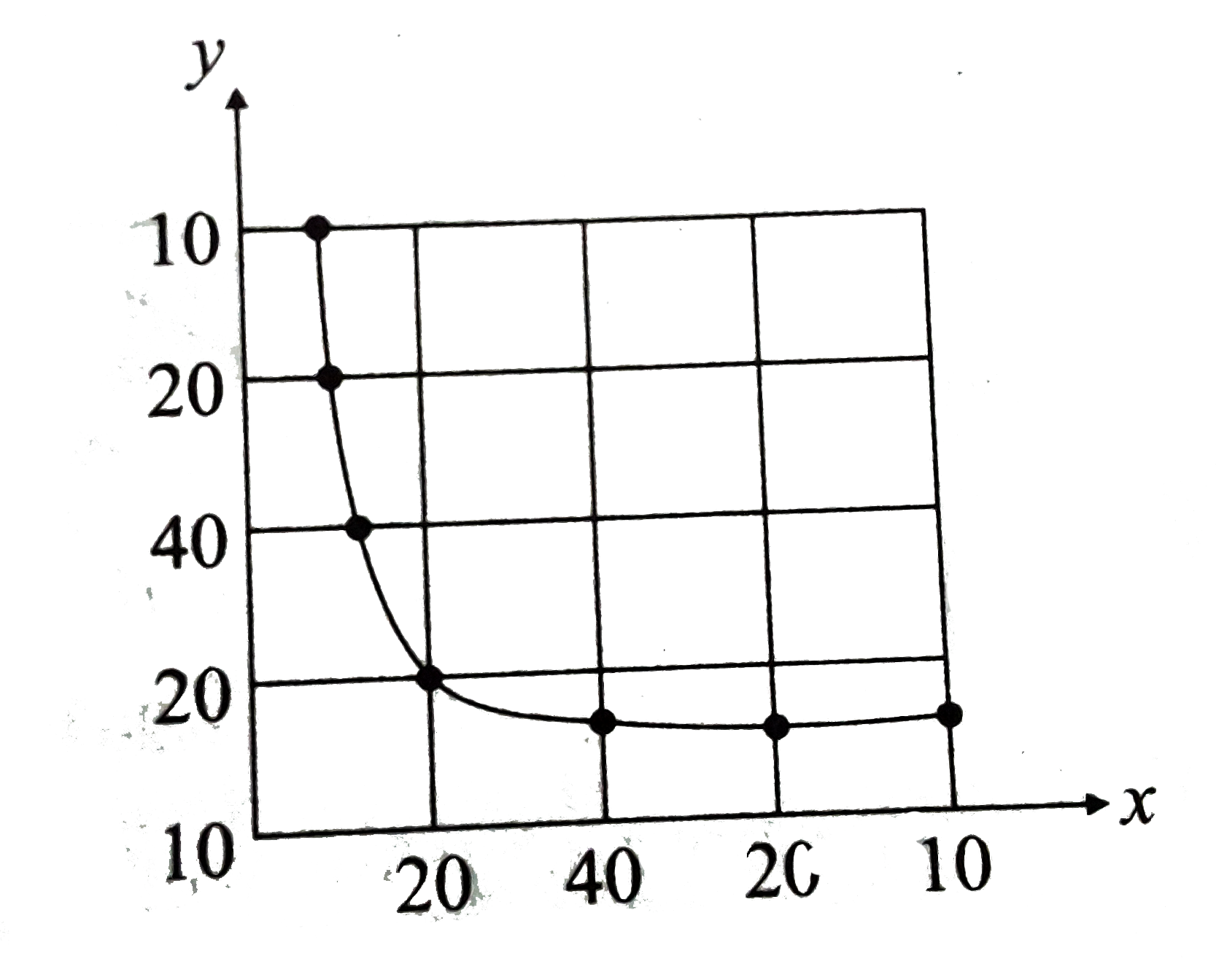
View SolutionIn an experiment for the determination of focal length of the convex mirror a convex lens of focal length 20cm is placed on the optical bench and an object pin is placed at a distance 30cm from the lens. When a convex mirror is introduced in between the lens and the real and inverted image of the object, the final image of object O is formed at O itself. If the distance between the lens and the mirror is 10cm, then the focal length of the mirror is
View SolutionA lens produces a virtual image between the object and the lens.
Name the lens.
View SolutionDraw a labelled ray diagram for the formation of image by a convex lens of focal length 15 cm when the object is placed at a distance of 25 cm from the lens. Determine the size of the image formed, if size of the object is 4 cm.
View SolutionA thin converging lens of focal length f = 25 cm forms the image of an object on a screen placed at a distance of 75 cm from the lens. Now the screen in moved closer to the lens by a distance of 25 cm. The distance through which the object has to be shifted so that its image on the screen is sharp again is
View Solution
