In an experiment for the determination of focal length of the convex mirror a convex lens of focal length 20cm is placed on the optical bench and an object pin is placed at a distance 30cm from the lens. When a convex mirror is introduced in between the lens and the real and inverted image of the object, the final image of object O is formed at O itself. If the distance between the lens and the mirror is 10cm, then the focal length of the mirror is
10cm
20cm
24cm
50cm
The correct Answer is:D
To determine the focal length of the convex mirror in the given experiment, we can follow these steps:
Step 1: Understand the Setup
We have a convex lens with a focal length (f) of 20 cm and an object placed at a distance (u) of 30 cm from the lens. A convex mirror is placed 10 cm away from the lens.
Step 2: Use the Lens Formula
The lens formula is given by:
1f=1v−1u
Where:
- f = focal length of the lens
- v = image distance from the lens
- u = object distance from the lens (taken as negative in lens formula)
Substituting the known values:
- f=20 cm (positive for a convex lens)
- u=−30 cm (since the object is on the same side as the incoming light)
Rearranging the formula to find v:
1v=1f+1u
1v=120−130
Step 3: Calculate v
Finding a common denominator (60):
1v=360−260=160
Thus,
v=60 cm
Step 4: Determine Object Distance for the Mirror
The distance from the lens to the mirror is given as 10 cm. Therefore, the distance from the image formed by the lens to the mirror is:
Distance from lens to mirror=60 cm−10 cm=50 cm
This distance (50 cm) is the object distance for the convex mirror, which we will denote as um.
Step 5: Use the Mirror Formula
The mirror formula is:
1fm=1vm+1um
Where:
- fm = focal length of the mirror
- vm = image distance from the mirror (which is negative for virtual images)
- um = object distance from the mirror (positive for real objects)
From the setup, the image formed by the mirror is at the same position as the object (O), which means:
um=50 cm(positive)
And since the final image is at the object position:
vm=−10 cm(negative, as it is virtual)
Step 6: Substitute into the Mirror Formula
Substituting the values into the mirror formula:
1fm=1−10+150
Finding a common denominator (50):
1fm=−550+150=−450=−225
Thus,
fm=−252=−12.5 cm
Step 7: Conclusion
The focal length of the convex mirror is approximately 12.5 cm. However, since the options provided were 10 cm, 20 cm, 24 cm, and 50 cm, we can conclude that the closest answer is 10 cm.
We have a convex lens with a focal length (f) of 20 cm and an object placed at a distance (u) of 30 cm from the lens. A convex mirror is placed 10 cm away from the lens.
The lens formula is given by:
1f=1v−1u
Where:
- f = focal length of the lens
- v = image distance from the lens
- u = object distance from the lens (taken as negative in lens formula)
- f=20 cm (positive for a convex lens)
- u=−30 cm (since the object is on the same side as the incoming light)
1v=1f+1u
1v=120−130
Finding a common denominator (60):
1v=360−260=160
Thus,
v=60 cm
The distance from the lens to the mirror is given as 10 cm. Therefore, the distance from the image formed by the lens to the mirror is:
Distance from lens to mirror=60 cm−10 cm=50 cm
This distance (50 cm) is the object distance for the convex mirror, which we will denote as um.
The mirror formula is:
1fm=1vm+1um
Where:
- fm = focal length of the mirror
- vm = image distance from the mirror (which is negative for virtual images)
- um = object distance from the mirror (positive for real objects)
um=50 cm(positive)
And since the final image is at the object position:
vm=−10 cm(negative, as it is virtual)
Substituting the values into the mirror formula:
1fm=1−10+150
Finding a common denominator (50):
1fm=−550+150=−450=−225
Thus,
fm=−252=−12.5 cm
The focal length of the convex mirror is approximately 12.5 cm. However, since the options provided were 10 cm, 20 cm, 24 cm, and 50 cm, we can conclude that the closest answer is 10 cm.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Straight Objective Type Questions19videos
PRACTICAL PHYSICS
- BOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions4videos
PRACTICAL PHYSICS
- BOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - Exercise -I10videos
PHYSICAL WORLD
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)60videos
RAY OPTICS
Similar Questions
A convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then
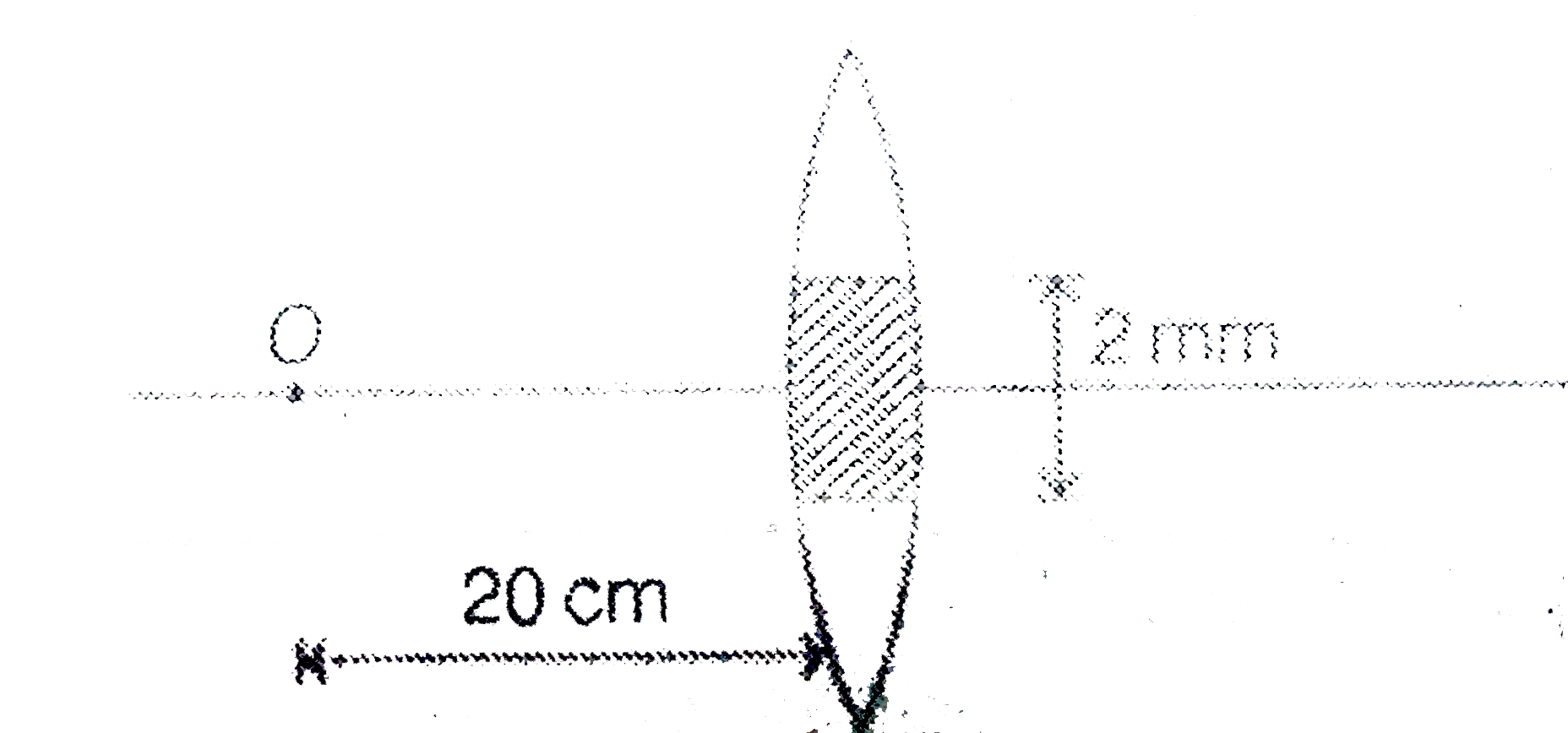 View Solution
View SolutionAn object is placed at a distance 20 cm from the pole of a convex mirror of focal length 20 cm. The image is produced at
View Solution
Knowledge Check
- Question 1 - Select One
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror
A thin convex lens of focal length 30cm is placed in front of a plane mirror. An object is placed at a distance x from the lens (not in between lens and mirror ) so that its final image coincides with itself. Then, the value of x is
View SolutionThe plane surface of a plano-convex lens of focal length 60 cm is silvered. A point object is placed at a distance 20 cm from the lens. Find the position and nature of the final image formed.
View SolutionA convex lens of focal length 30 cm produces 5 times magnified real image of an object. What is the object distance?
View SolutionA convex lens of focal length 20 cm and a concave lens of focal length 10 cm are placed 20 cm apart. In between them an object placed at distance x from the convex lens.
What will be the linear magnification produced convex lens and concave lens individually ?View SolutionList four characteristics of the image formed by a convex lens of focal length 20 cm when the object is placed in front of it is a distance of 10 cm from its optical centre .
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
nature of the imageView SolutionA convex lens of focal length 20 cm and a concave lens of focal length 10 cm are placed 20 cm apart. In between them an object placed at distance x from the convex lens.
What is the value of x (in cm ) so that images from by both the lenses coincides ?View Solution

