A lens having focal length f and aperture of diameter d forms an image of intensity I. Aperture of diameter d/2 in central region of lens is covered by a black paper. Focal length of lens and intensity of image now will be respectively
f and I4
3f4 and I2
f and 3I4
f2 and I2
The correct Answer is:C
To solve the problem, we need to analyze the effect of covering the central region of a lens with a black paper, which reduces the aperture size. We will determine how this affects the focal length of the lens and the intensity of the image formed.
1. Understanding the Initial Conditions:
- We have a lens with a focal length f and an aperture of diameter d.
- The lens forms an image with intensity I.
2. Effect of Reducing the Aperture:
- When the central region of the lens with diameter d/2 is covered, the effective aperture diameter is reduced to d/2.
- The radius of the aperture also changes; it becomes r=d4 (since radius is half of the diameter).
3. Calculating the Area of the Aperture:
- The area of the original aperture (diameter d) is given by:
A=π(d2)2=πd24
- The area of the new aperture (diameter d/2) is:
A′=π(d/22)2=π(d4)2=πd216
4. Comparing Areas:
- The new area A′ is one-fourth of the original area A:
A′=A4
5. Effect on Intensity:
- Intensity I is proportional to the area of the aperture. Therefore, if the area is reduced to one-fourth, the intensity will also reduce to one-fourth:
I′=I4
6. Final Intensity Calculation:
- The new intensity I′ is:
I′=I4
7. Effect on Focal Length:
- The focal length f of the lens does not depend on the size of the aperture. It is determined by the lens material and its curvature.
- Therefore, the focal length remains unchanged:
f′=f
Conclusion:
- The new focal length of the lens remains f.
- The new intensity of the image becomes I4.
Final Answer:
- Focal length: f
- Intensity: I4
- We have a lens with a focal length f and an aperture of diameter d.
- The lens forms an image with intensity I.
- When the central region of the lens with diameter d/2 is covered, the effective aperture diameter is reduced to d/2.
- The radius of the aperture also changes; it becomes r=d4 (since radius is half of the diameter).
- The area of the original aperture (diameter d) is given by:
A=π(d2)2=πd24
- The area of the new aperture (diameter d/2) is:
A′=π(d/22)2=π(d4)2=πd216
- The new area A′ is one-fourth of the original area A:
A′=A4
- Intensity I is proportional to the area of the aperture. Therefore, if the area is reduced to one-fourth, the intensity will also reduce to one-fourth:
I′=I4
- The new intensity I′ is:
I′=I4
- The focal length f of the lens does not depend on the size of the aperture. It is determined by the lens material and its curvature.
- Therefore, the focal length remains unchanged:
f′=f
- The new focal length of the lens remains f.
- The new intensity of the image becomes I4.
- Focal length: f
- Intensity: I4
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Reflection Of Light By Spherical Mirrors
5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Refraction
10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSERTION AND REASON
15 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A thin lens focal length f and its aperture has diameter d. It forms an image of intensity I. Now the central part of the aperture up to diameterd2 is blocked by an opaque paper. The focal length and image intensity will change to
View SolutionA convex lens has a focal length of 20 cm. It is used to form an image of an object placed 15 cm from lens. The image is
View SolutionAn object is placed at a distance of f2 from a convex lens of focal length f. The image will be
View SolutionA convex lens of focal length 30 cm forms an image of height 2 cm for an object situated at infinity. If a concave lens of focal length 20 cm is placed coaxially at a distance of 26 cm from convex lens then size of image would be
View SolutionShown an object and its image formed by a thin lens. Then the nature and focal length of lens is
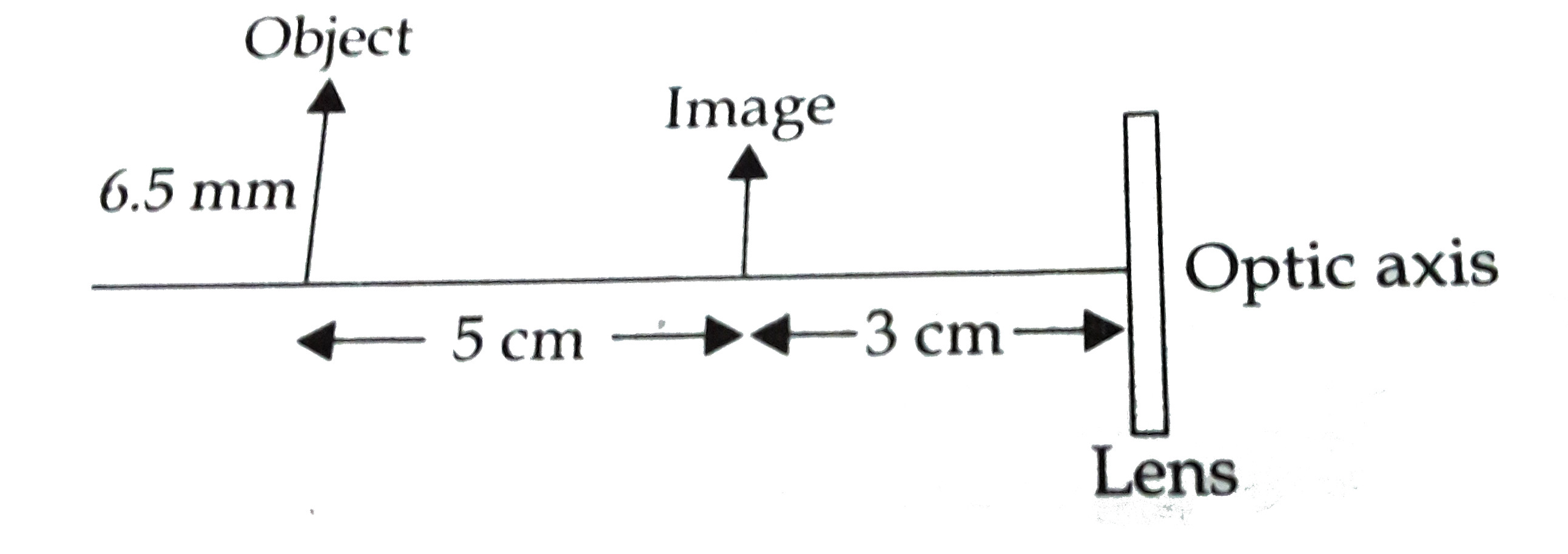
View SolutionFind the focal length of the lens used to focus an image of distant object on focal plane of the lens if the radius of central bright dot is 5μm, when it illuminated by ray of wavelength 400 nm and the radius of the circular aperture is 2.5 cm.
View SolutionDraw ray diagrams showing the image formation by a convex lens when an object is placed
(a) between optical centre and focus of the lens
(b) between focus and twice the focal length of the lens
( c) at twice the focal length of the lens
(d) at infinity , (e) at the focus of the lens
View SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
View SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
View SolutionGraph of position of image vs position of point object from a convex lens is shown. Then, focal length of the lens is
_E01_287_Q01.png)
View Solution
