A lens of diameter 5.0cm and focal length f=25.0cm was cut along the diameter into two identical halves. In the process, the layer of the lens α=1.00mm in thieckness was lost. Then the halves were put together to form a composite lens. In this focal plane a narrow slit was placed, emitting monochromatic light with wavelength λ=0.60μm. Behind the lens a screen was located at a distance b=50cm from it. Find:
(a) the which of a fringe on the screen and the number of possible maxima,
(b) the maximum width of the slit ∂max at which the fringes on the screen will be still observed sufficiently sharp.

(a) We show the upper half o fthe lens. The emergent light is at an angle a2f from the axis.
Thus the divergence angle of the two incident light beams is
ψ=af
When they interfere the fringes produced have a width
Δx=λψ=fλa=0.15mm.
The patch on the screen illuminated by both light has s width bψ and this contains
bψΔx=ba2f2λ fringes =13 fringes
(if we ignore 1 in comparies on to bψΔx (if 5.71(a))
(b) We follow the logic of. From one edge of the slit to the edge the distance is of magnitude ∂ (i.e a2 to a2+∂).
If we imagine teh edge to shift by this distance, the angle ψ/2 will increase by Δψ2=∂2f
and the light will shift ±b∂2f
The fringe patten will therefore shift by ∂.bf
Equating this to δx2=fλ2a we get ∂max=f2λ2ab=37.5μm.
Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Diffraction Of Light
60 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Polarization Of Light
43 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
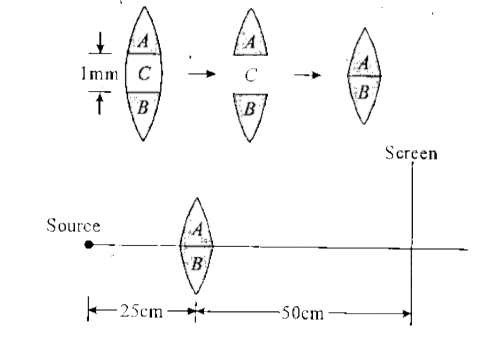
In Billet's Lens Arrangement, a convex lens of focal length 50 cm is cut along the diameter into two indentical halves Å and B and in the process a layer C of the lens thickness 1 mm is lost. Then the two halves A and B are put together to form a composite lens. Now, infront of this composite lens a source of light emitting wavelength λ=6000Å is placed at a distance of 25 cm as shown in the figure. Behind the lens there is a screen at a distance 50 cm from it. Find the fringe width fo the interference pattern obtained on the screen.
View SolutionAn equiconvex lens of focal length 15cm is cut into two equal halves in thickness. What is the focal length of each half ?
View Solution
Knowledge Check
A lens of focal length f is cut along the diameter into two identical halevs. In this process, a layer of the lens t in thickness is lost, then the halves are put together to form a composite lens. In between the focal plane and the composite lens, a narrow slit is placed near the focal plane. The slit is emitting monochromatic λ. Behind the lens, a screen is located at a distance L front it.

Find the fringe width for the pattern obtained under given arrangement on the screen.Aλf2tBλftCtfλDtfλ2A lens of focal length f is cut along the diameter into two identical halevs. In this process, a layer of the lens t in thickness is lost, then the halves are put together to form a composite lens. In between the focal plane and the composite lens, a narrow slit is placed near the focal plane. The slit is emitting monochromatic λ. Behind the lens, a screen is located at a distance L front it.
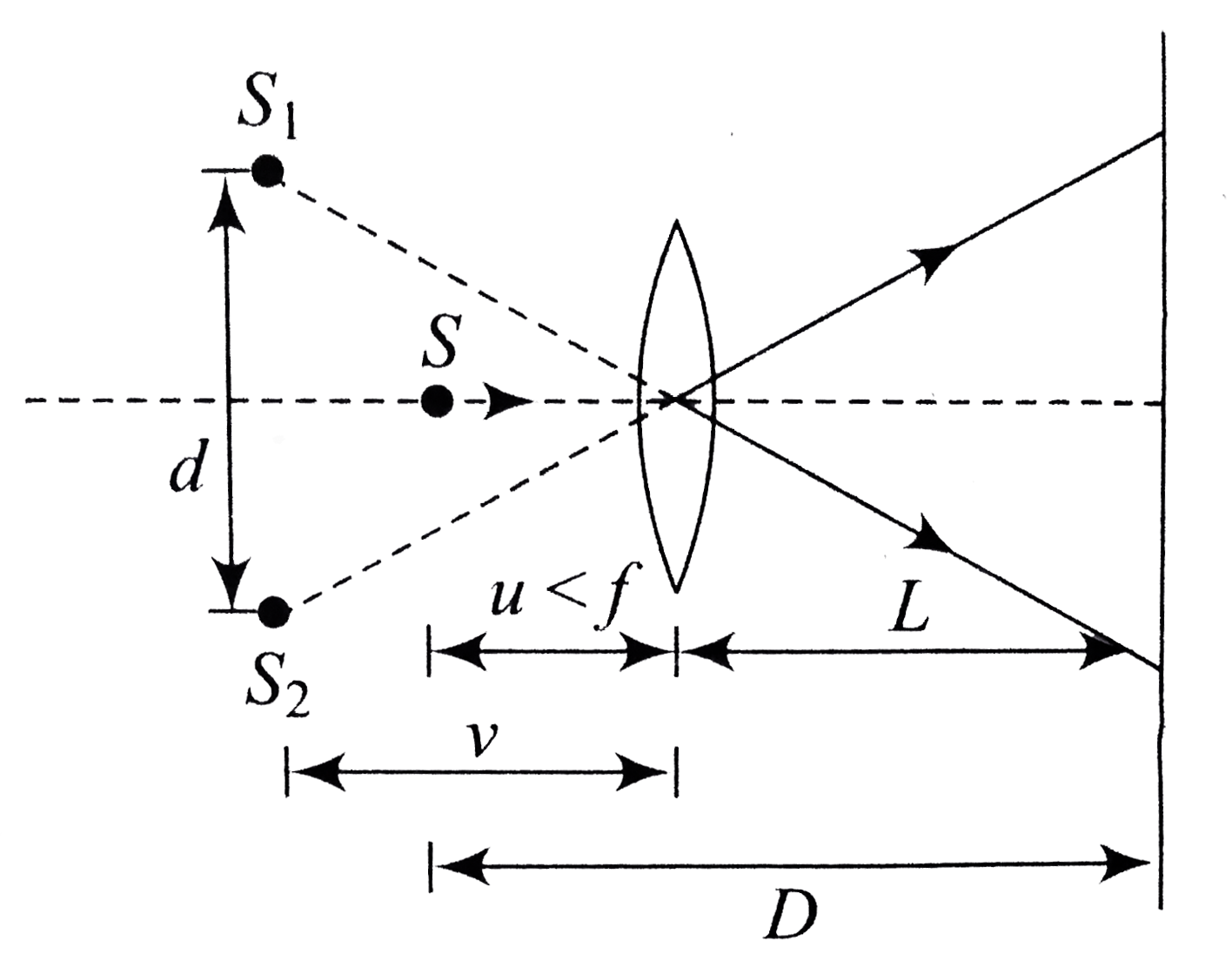
The expression for the number of visible maxima which are obtained through above said arrangement will turn out to beALt2λf2B2Lt2λf2CLt2λf2DLt22λf2The focal length of a lens is 0.1 m. Then the lens must be
AconvexBconcaveCcylindricalDnone of these
If the focal length of the biconvex lens is 25 cm, then the
power of the lens will be
View SolutionThe power of a lens of focal length 0.5 m is :
View SolutionThe power of a lens of focal length 0.5 m is :
View SolutionA convex lens of Focal length of 40cm is in contact with a concave lens of focal length 25cm. The power of the combination is.
View SolutionA convex lens of focal length 40 cm is in contact with a concave lens of foal length 25 cm. The power of the lens combination is
View Solution
