A light filter is a plate of thickness d whose absorption coefficient depends on wavelength λ as
x(λ)=α(1−λ/λ0)2cm−1,
where α and λ0 are constants. Find the passband Δλ of this light filter, that is the band at whose edge the attenuation of light is η times that at the wavelength λ0. The coefficient of reflection from teh surfaces of the light filter is assumed to be the same at all wavelengths.
At the wavelength λ0 the absotption coeffcient vanishes and loss intransmission is entirely due to reflection. This factor is the same at all wavelengths and therefore cancels out in calculating the pass bank and we need not worrt about it. Now
T0= (transmissivity al λ=λ0)=(1−ρ)2
T= transmissivity at λ=(1−ρ)2e−χ(λ)d
The edges of the passband are λ0±Δλ2 and at the edge
TT0=e−αd(Δλ2λ0)2=η
Thus δλ2λ0=√(In1η)/∝d
or Δλ=2λ0√1αd(In1η)
Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Optics Of Moving Sources
22 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Thermal Equation
47 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Polarization Of Light
43 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
A light filler 5 mm thick has a variable absorption coefficient which depends on the wavelength according to the law μ=μo+a(λo−λ)2 where a=5.6X1020m−3λo=5000λμo=4m−1.Find the transmithance, of the filter for the wavelongth λo and its transmission band width
View SolutionThe refractive index of light in glass varies with its wavelength according to equation
μ(λ)=a+bλ2 where a and b are positive constants.
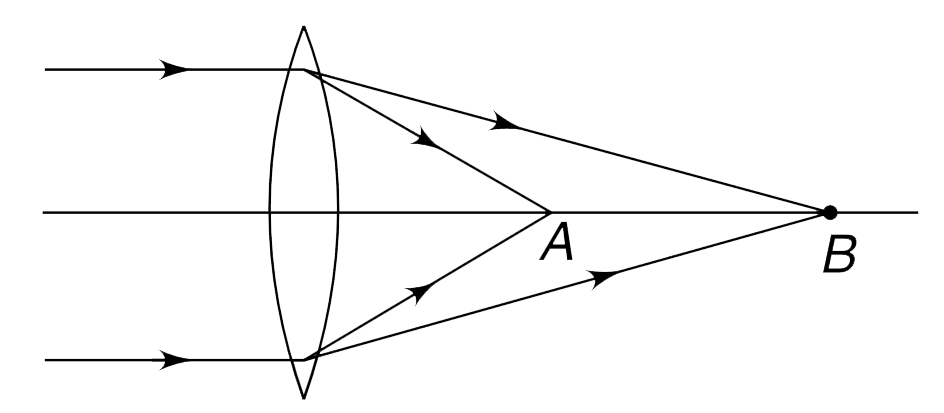
A nearly monochromatic parallel beam of light is incident on a thin convex lens as shown. The wavelength of incident light is λ0±Δλ where Δλ<<λ0. The light gets focused on the principal axis of the lens over a region AB. If the focal length of the lens for a light of wavelength λ0 is f0, find the spread AB.
View Solution
Knowledge Check
The wavelength of light in vacuum is λ. The wavelength of light in a medium of refractive index n will be
AnλBλnCλn2Dn2λFor balmer series wavelength of first line is λ1 and for brackett series wavelength of first line is λ2 then λ1λ2 is
A0.81B0.162C0.198D0.238For balmer series wavelength of first line is λ1 and for brackett series wavelength of first line is λ2 then λ1λ2 is
A0.81B0.162C0.198D0.238
A beam of light of intensity I0 falls normally on a transparent plane-parallel plate of thickness l. The beam contains all the wavelengths in the interval from λ1 to λ2 of equal spectral intensity. Find the intensity of the transmitted beam if in this wavelength interval the absorption coefficient is a linear function of λ, with exterme values x1 and x2. The coefficient of reflection at each surfcae is equal to ρ. The secondary reflections are to be neglected.
View SolutionWhen a metal is illuminated by light of wavelength λ , the stopping potential is V∘ and for wavelength 2λ, it is 3V∘.Then the threshold wavelength is ?
View SolutionLet be the maximum kinetic energy of photoelectrons emitted by light of wavelength λ1 and λ2 correspondingto wavelength λ2. If λ1=2λ2 then:
View SolutionThe wavelength of light in air and some other medium are respectively λa and λm. The refractive index of medium is
View Solutionif λv',λx and λm represent the wavelengths of visible light X-rays and microwaves respectively then:
View Solution
