A light filler 5 mm thick has a variable absorption coefficient which depends on the wavelength according to the law μ=μo+a(λo−λ)2 where a=5.6X1020m−3λo=5000λμo=4m−1.Find the transmithance, of the filter for the wavelongth λo and its transmission band width
The correct Answer is:98%; 10 A.
Suppose white light of intensity I∈=A2 falls on the light fillter. At the resonance wavelength λ0 the intersity of the transmitted light will be I0I0 =… The intensity of transmitted light of other wavelengths will be
I=A2e−μd=A2e−μ0de−αd(λ0−λ)2=I0e−αd(λ0−λ)^2
we are interested in the case when
when e−αd(λ0−λ)2>–––2−1
Taking logarithms , we obtain αd(λ0−λ)>–––– In 2, giving λb=λ0±√ln2αd. the width of the spectral interval is Δλ=2√ln2αd .
The transmittance at the resonance wavelength is k0=I0/A2=e−μ0d.
Similar Questions
A light filter is a plate of thickness d whose absorption coefficient depends on wavelength λ as
x(λ)=α(1−λ/λ0)2cm−1,
where α and λ0 are constants. Find the passband Δλ of this light filter, that is the band at whose edge the attenuation of light is η times that at the wavelength λ0. The coefficient of reflection from teh surfaces of the light filter is assumed to be the same at all wavelengths.
View SolutionThe refractive index of light in glass varies with its wavelength according to equation
μ(λ)=a+bλ2 where a and b are positive constants.
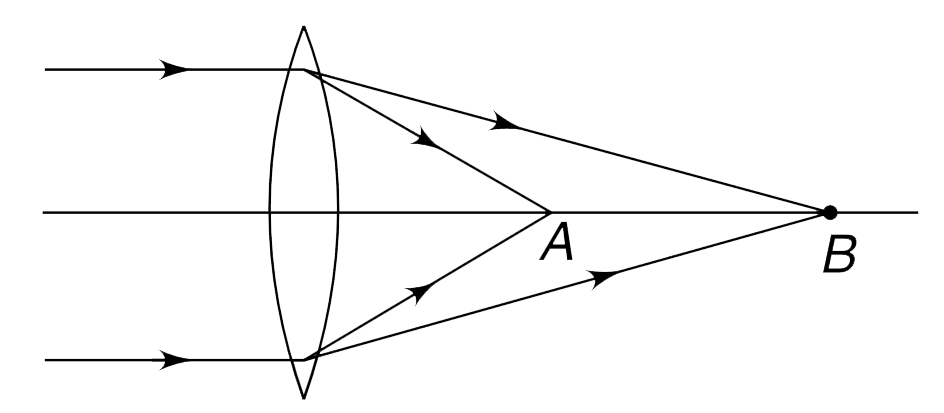
A nearly monochromatic parallel beam of light is incident on a thin convex lens as shown. The wavelength of incident light is λ0±Δλ where Δλ<<λ0. The light gets focused on the principal axis of the lens over a region AB. If the focal length of the lens for a light of wavelength λ0 is f0, find the spread AB.
View Solution
Knowledge Check
A plane wave of monochromatic light falls normally on a uniform thin or oil which covers a glass plate. The wavelength of source can be varied continuously. Complete destructive is observed for λ=5000Å and λ=1000Å and for no other wavelength in between. If μ of oil is 1.3 and that of glass is 1.5, the thickness of the film will be
A6.738×10(−5)cmB5.7×10−5cmC4×10−5cmD2.8×10−5cm
ABC is a triangle and A=(2,3,5),B=(-1,3,2) and C= (λ,5,μ). If the median through A is equally inclined to the axes, then find the value of λ and μ
View SolutionABC is a triangle and A=(2,3,5),B=(-1,3,2) and C= (λ,5,μ). If the median through A is equally inclined to the axes, then find the value of (λ,μ)
View SolutionThe existence of the unique solution of the system of equations: x+y+z=λ
5x−y+μz=2
2x+3y−z=6 d e p e n d s on μonly (b) λonly λandμ⊥h (d) neitherλ∥u∥
View SolutionA plane wave of monochromatic light falls normally on a uniform thin or oil which covers a glass plate. The wavelength of source can be varied continuously. Complete destructive is observed for λ=5000Å and λ=1000Å and for no other wavelength in between. If μ of oil is 1.3 and that of glass is 1.5, the thickness of the film will be
View Solution∫2(2−x)2(2−x2+x)1/3dx=λ(2+x2−x)μ+c where λandμ are rational number in its simplest form then (λ+1μ) is equal to
View SolutionIf ∫2(2−x)2(2−x2+x)1/3 dx=λ(2+x2−x)μ+c where λandμ are rational number in its simplest form then (λ+1μ) is equal to
View SolutionIn a Young's double slit experiment, one of the slits is covered by a thin film of thickness t=0.04 mm, and refractive index μ=1.2+9×10−14m2λ2, where λ is the wavelength in meter. A beam of light consisting of two wavelength λ1=400nmandλ2=600nm falls normally on the plane of the slits. Find the distance between two central maxima in milimeter. Distance of screen from slits is 400 times the the separation between the slits.
View Solution
