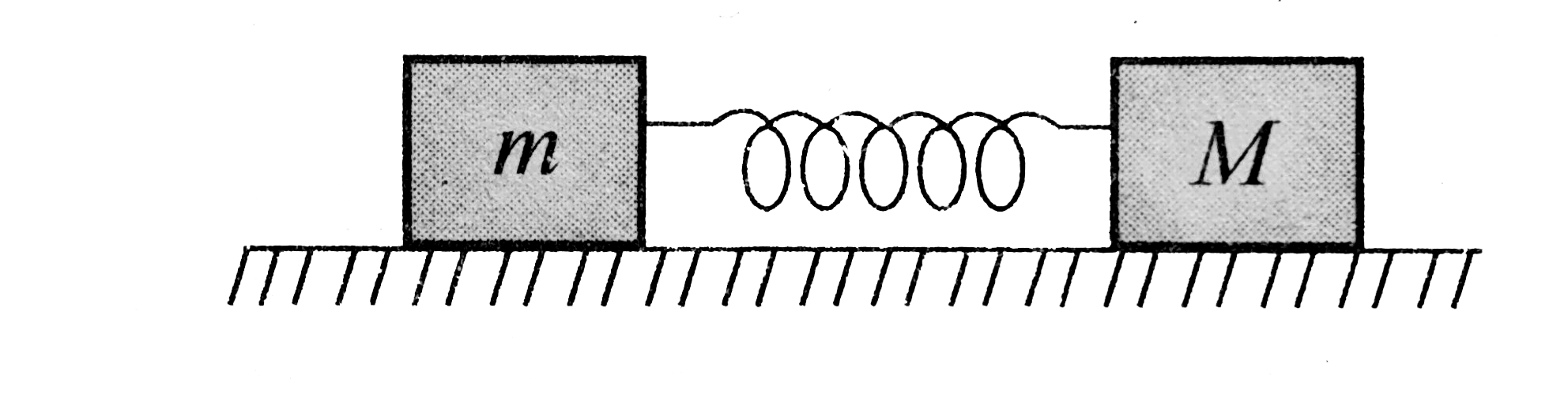
A light spring of constant $k$ is kept compressed between two blocks of masses $m$ and $M$ on a smooth horizontal surface. When released, the block acquire velocities in opposite directions. The spring loses contact with the blocks when it acquires natural length. if the spring was initially compressed through a distance $x$ , find the final speeds of the two blocks.

Video Solution

Text Solution

Verified by Experts

Consider the two blocks plus the spring to the the system, no external force acts on this suystem in horizontal direction. Hence the linear momentum will remain constant. Suppose, the block of mass $M$ moves with a speed $V$ and the other block with a speed $v$ after losing contact with spring. From conservation of linear momentum in horizontal direction, we have
$M V - m v = 0$ or $V = \frac{m v}{M}$ ........i
Initially, the mechanical energy of the system $= \frac{1}{2} M V^{2}$
finally the mechanical energy of the system $= \frac{1}{2} m v^{2} + \frac{1}{2} M V^{2}$
As there is no friction, mechaical energy will remain conserved, therefore, $\frac{1}{2} m^{2} + \frac{1}{2} M V^{2} = \frac{1}{2} k^{2}$ .........ii
Solving Eqn i and ii, we get
$v = {[\frac{k M}{m (M + m)}]}^{\frac{1}{2}} x$
and $V = {[\frac{k M}{M (M + m)}]}^{\frac{1}{2}} x$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A light spring of force constant 'K' is held between two blocks of masses 'm' and '2m'. The two blocks and the spring system rests on a smooth horizontal floor. Now th blocks are moved towards each other compressing the springs by 'x' and suddenly released. The relative velocity between the blocks when the spring attains its natural length will be
A $(\sqrt{\frac{3 K}{2 m}}) x$
B $(\sqrt{\frac{2 K}{3 m}}) x$
C $(\sqrt{\frac{K}{3 m}}) x$
D $(\sqrt{\frac{K}{2 m}}) x$
Question 2 - Select One
Two blocks of masses $m_{1}$ and $m_{2}$ are kept on a smooth horizontal table as shown in figure. Block of mass $m_{1}$ (but not $m_{2}$ is fastened to the spring. If now both the blocks are pushed to the left so that the spring is compressed a distance d. The amplitude of oscillatin of block of mass $m_{1}$ after the system is released is

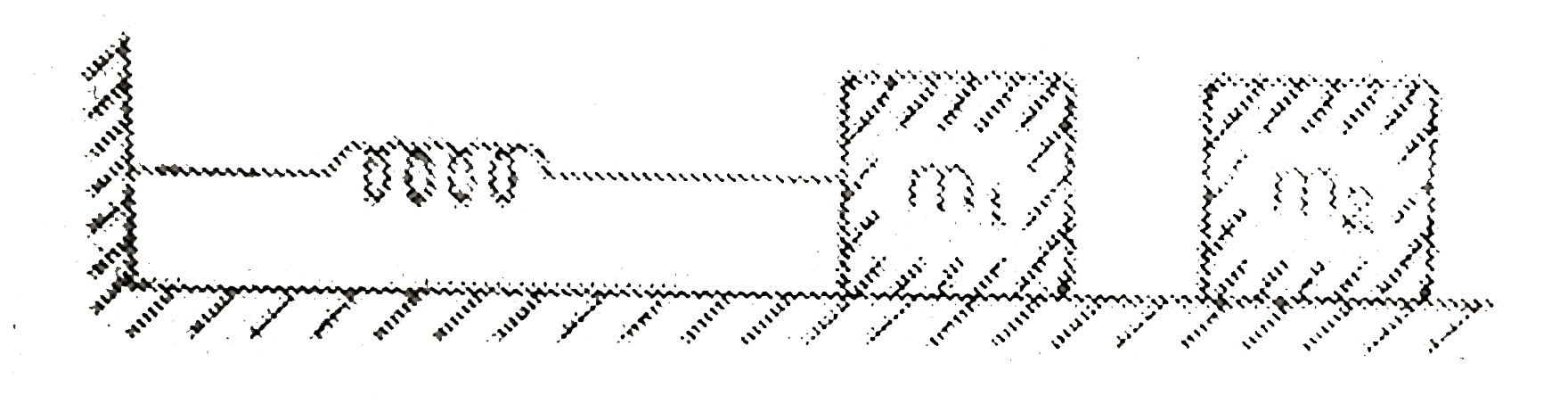A $d \sqrt{\frac{m_{1}}{m_{1} + m_{2}}}$
B $d \sqrt{\frac{m_{2}}{m_{1} + m_{2}}}$
C $d \sqrt{\frac{2 m_{2}}{m_{1} + m_{2}}}$
D $d \sqrt{(2 \frac{m_{1}}{m_{1} + m_{2}}}$
Question 3 - Select One
A block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
A $v \sqrt{m / 2 k}$
B $v \sqrt{m / k}$
C $v \sqrt{m / 4 k}$
D $m v^{2} / 4 k$

CENGAGE PHYSICS-CENTRE OF MASS-INTEGER_TYPE

Home
Ask Doubt
Profile