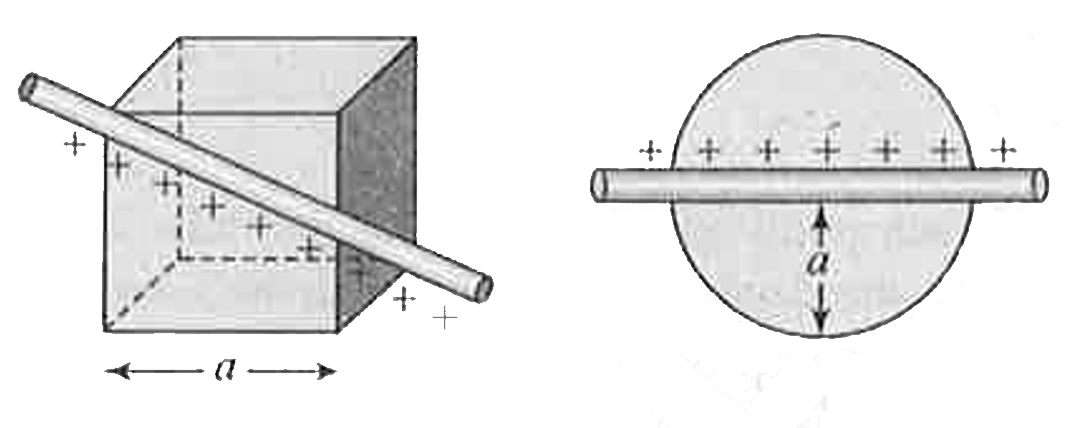
A linear charge having linear charge density λ, penetrates a cube diagonally and that it penetrates a sphere diametrically as shown. The ratio of flux coming out of the cube and the sphere is √xy, Find (xy).
'(##CEN_KSR_PHY_JEE_C18_E01_011_Q03##)'
The correct Answer is:6
To find the ratio of the electric flux coming out of a cube and a sphere when a linear charge with linear charge density λ penetrates both shapes, we can follow these steps:
Step 1: Understand the Geometry
- The linear charge penetrates the cube diagonally and the sphere diametrically.
- The length of the cube's diagonal can be represented as l√3, where l is the side length of the cube.
- The diameter of the sphere is 2R, where R is the radius of the sphere.
Step 2: Calculate the Charge Enclosed
- For the cube:
- The charge enclosed by the cube is given by:
Qc=λ⋅l√3
- For the sphere:
- The charge enclosed by the sphere is given by:
Qs=λ⋅2R
Step 3: Apply Gauss's Law
- According to Gauss's Law, the electric flux Φ through a closed surface is given by:
Φ=Qenclosedϵ0
- For the cube, the electric flux Φc is:
Φc=Qcϵ0=λl√3ϵ0
- For the sphere, the electric flux Φs is:
Φs=Qsϵ0=λ⋅2Rϵ0
Step 4: Find the Ratio of Fluxes
- The ratio of the electric fluxes is:
ΦcΦs=λl√3ϵ0λ⋅2Rϵ0=l√32R
Step 5: Substitute Values
- If we assume l=R (the side of the cube is equal to the radius of the sphere), then:
ΦcΦs=R√32R=√32
Step 6: Identify x and y
- From the ratio ΦcΦs=√32, we can identify x=3 and y=2.
Step 7: Calculate xy
- Therefore, xy=3⋅2=6.
Final Answer
The value of xy is 6.
---
- The linear charge penetrates the cube diagonally and the sphere diametrically.
- The length of the cube's diagonal can be represented as l√3, where l is the side length of the cube.
- The diameter of the sphere is 2R, where R is the radius of the sphere.
- For the cube:
- The charge enclosed by the cube is given by:
Qc=λ⋅l√3
- For the sphere:
- The charge enclosed by the sphere is given by:
Qs=λ⋅2R
- According to Gauss's Law, the electric flux Φ through a closed surface is given by:
Φ=Qenclosedϵ0
- For the cube, the electric flux Φc is:
Φc=Qcϵ0=λl√3ϵ0
- For the sphere, the electric flux Φs is:
Φs=Qsϵ0=λ⋅2Rϵ0
- The ratio of the electric fluxes is:
ΦcΦs=λl√3ϵ0λ⋅2Rϵ0=l√32R
- If we assume l=R (the side of the cube is equal to the radius of the sphere), then:
ΦcΦs=R√32R=√32
- From the ratio ΦcΦs=√32, we can identify x=3 and y=2.
- Therefore, xy=3⋅2=6.
The value of xy is 6.
Topper's Solved these Questions
Similar Questions
A linear charge having linear charge density λ, penetrates a cube diagonally and that it penetrates a sphere diametrically as shown. The ratio of flux coming out of the cube and the sphere is √xy, Find (xy).
'(##CEN_KSR_PHY_JEE_C18_E01_011_Q03##)'
View SolutionThe ratio of time constant in charging and discharging in the circuit shown in the figure is xy. Find (x+y)
'(##CEN_KSR_PHY_JEE_CO23_E01_034_Q12##)'
View Solution
Knowledge Check
A linear charge having linear charge density λ pentrates a cube diagonally and then it pentrates a spere diametrically as shown. What will br the ratio of flux coming out of cube and sphere ?
 A12B2√3C√32D11
A12B2√3C√32D11
A satellite S moves around a planet P in an elliptical orbit as shown in the figure. The ratio of the speed of the satellite at point a to that at point b is xy, Find (x−y).
'(##CEN_KSR_PHY_JEE_C10_011_Q01##)'
View SolutionIn the shown figure, the focal length of equivalent system is 50x13. Find the value of x.
'(##CEN_KSR_PHY_JEE_C26_E01_020_Q07##)'
View SolutionOne cycle of an altemating curreat is shown in the graph. The rms vatue of the current from t=0 to t=T is √2xi9. Find x.
'(##CEN_KSR_PHY_JEE_C24_E01_007_Q04##)'
View SolutionAn infinitely long string uniformly charged with a linear charge density λ1=1μC/m and a segment of length I uniformly charged with linear charge density λ2=1ln4μ C/M lie in a plane at right angle to each other and separated by a distance lassbown∈thefigure.Determinetheforce (in mN ) with which these two intertct.
'(##CEN_KSR_PHY_JEE_C18_E01_035_Q20##)'
View SolutionA thermodynamic process undergoes a cyclic process as shown. Find the quantity of heat supplied (in joule) to the system in one complęte cycle.
'(##CEN_KSR_PHY_JEE_C15_E01_004_Q03##)'
View SolutionThe graph below shows a particle in simple harmonic motion. From the information shown, find the value of time t1(in S).
'(##CEN_KSR_PHY_JEE_C16_E01_010_Q03##)'
View SolutionThe figure shows two paths through which a gas can be taken from state A to state B. If the ratio of work done by the gas in the two paths is xy, then find (x+y).
'(##CEN_KSR_PHY_JEE_C15_E01_001_Q01##)'
View Solution
