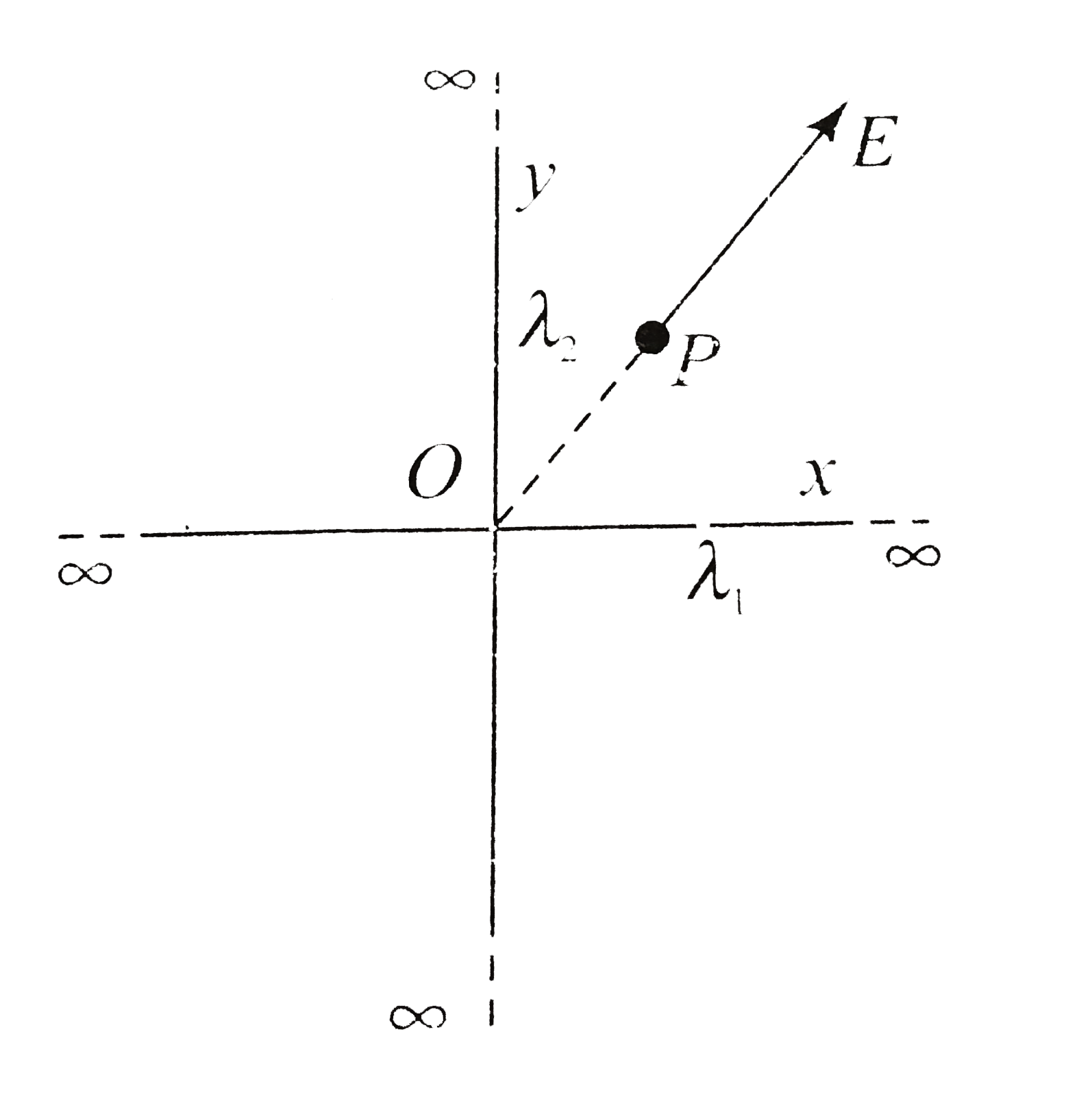
Two mutually perpendicular infinite wires along -axis and -axis carry charge densities and , respectively. The electric line of force at is along, the line , where is also a point lying on the same line. Find .
'(##CEN_KSR_PHY_JEE_C18_E01_025_Q12##)'
The correct Answer is:3
Topper's Solved these Questions
Similar Questions
Two mutually perpendicular infinite wires along x-axis and y-axis carry charge densities λ1 and λ2 (see figure). The 1 electric line of force at P is along the line y=1√3x, where P is also a point lying on the same line, then find λ1/λ2

View SolutionTwo mutually perpendicular infinite wires along x-axis and y-axis carry charge densities λ1andλ2. The electric line of force at P is along the line y=x/(√3), where P is also a point lying on the same line. Find λ2/λ1.
View Solution
Knowledge Check
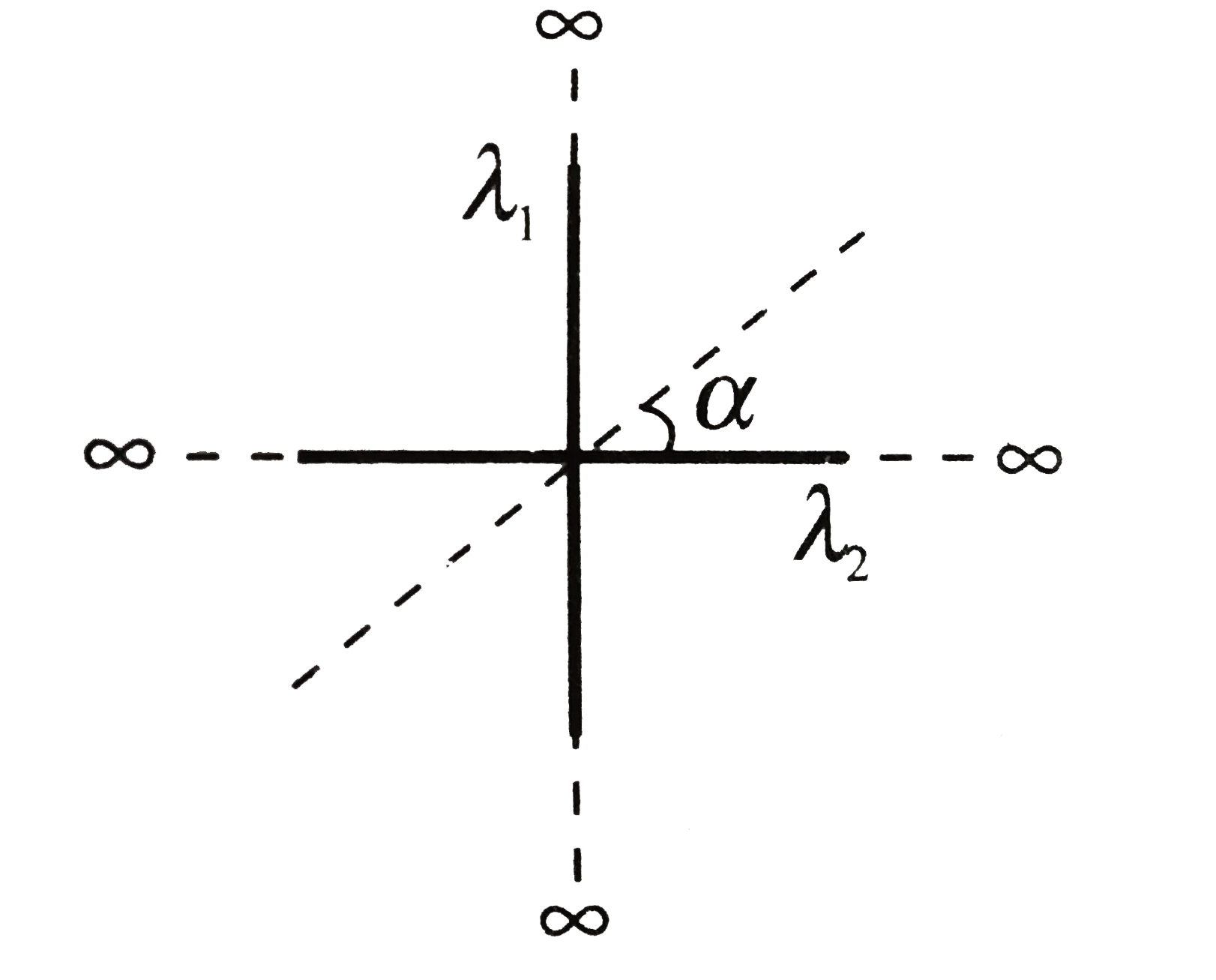
Two mutually perpendicular wire carry charge densities λ1andλ2. The electric lines of force makes angle α with second wire, then λ1/λ2 is
 Atan2αBcot2αCsin2αDcos2α
Atan2αBcot2αCsin2αDcos2αTwo uniformly long charged wires with linear densities λ and 3λ are placed along X and Y axis respectively. Determined the slope of electric field at any point on the l ine y=√3x
A3√3B√33√2C13√3D√3
Two mutually perpendicular infinite wires along x-axis and y-axis carry charge densities λ1andλ2. The electric line of force at P is along the line y=x/(√3), where P is also a point lying on the same line. Find λ2/λ1.

View SolutionTwo mutually perpendicular wire carry charge densities λ1andλ2. The electric lines of force makes angle α with second wire, then λ1/λ2 is

View SolutionTwo uniformly long charged wires with linear densities λ and 3λ are placed along X and Y axis respectively. Determined the slope of electric field at any point on the l ine y=√3x
View SolutionA wire AMB is placed along y-axis having linear charge density λ C/m. The electric field intensity at point P is ( PM=0.1 m)
View SolutionLinear charge densities of the two rods are given as λ1=−λ0xI2 and λ2=+λ0yl2. If the dipole moment of the system of rods is √mλ0ln, then find (m+n).
'(##CEN_KSR_PHY_JEE_C18_E01_009_Q02##)'
View SolutionA semi-circular wire is charged with linear charge density dependent on the angle θ from +y -axis as λ=λ0|sinθ|, where λ0 is a constant. The electric field intensity at the center of the arc is ¯¯¯E=mKλ04R(−ˆj). Find m.(R is the radius of semi-circle and K=14πɛ0)
'(##CEN_KSR_PHY_JEE_C18_E01_033_Q18##)'
View Solution
