A liquid having density $6000 k g / m^{3}$ stands to a height of $4 m$ in a sealed tank as shown in the figure. The tank contains compressed air at a gauge pressure of $3 a t m$ . The horizontal outlet pipe has a cross-sectional area of $6 c m^{2}$ and $3 c m^{2}$ at larger and smaller sections. Atmospheric pressure $= 1 a t m, g = 10 m / s^{2} 1 a t m = 10^{5} N / m^{2}$ .

Assume that depth of water in the tank remains constant due to $s$ very large base and air pressure above it remains constant. Based on the above information, answer the following questions.
The discharge rate from the outlet is

$4.02 \times 10^{- 3} m^{3} / s$

$6 \times 10^{- 5} m^{3} / s$

$7.56 \times 10^{- 3} m^{3} / s$

$4.02 \times 10^{- 5} m^{3} / s$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Let atmospheric pressure be $p_{0}$ . Then absolute pressure of air is $p + p_{0} = 4 a t m$

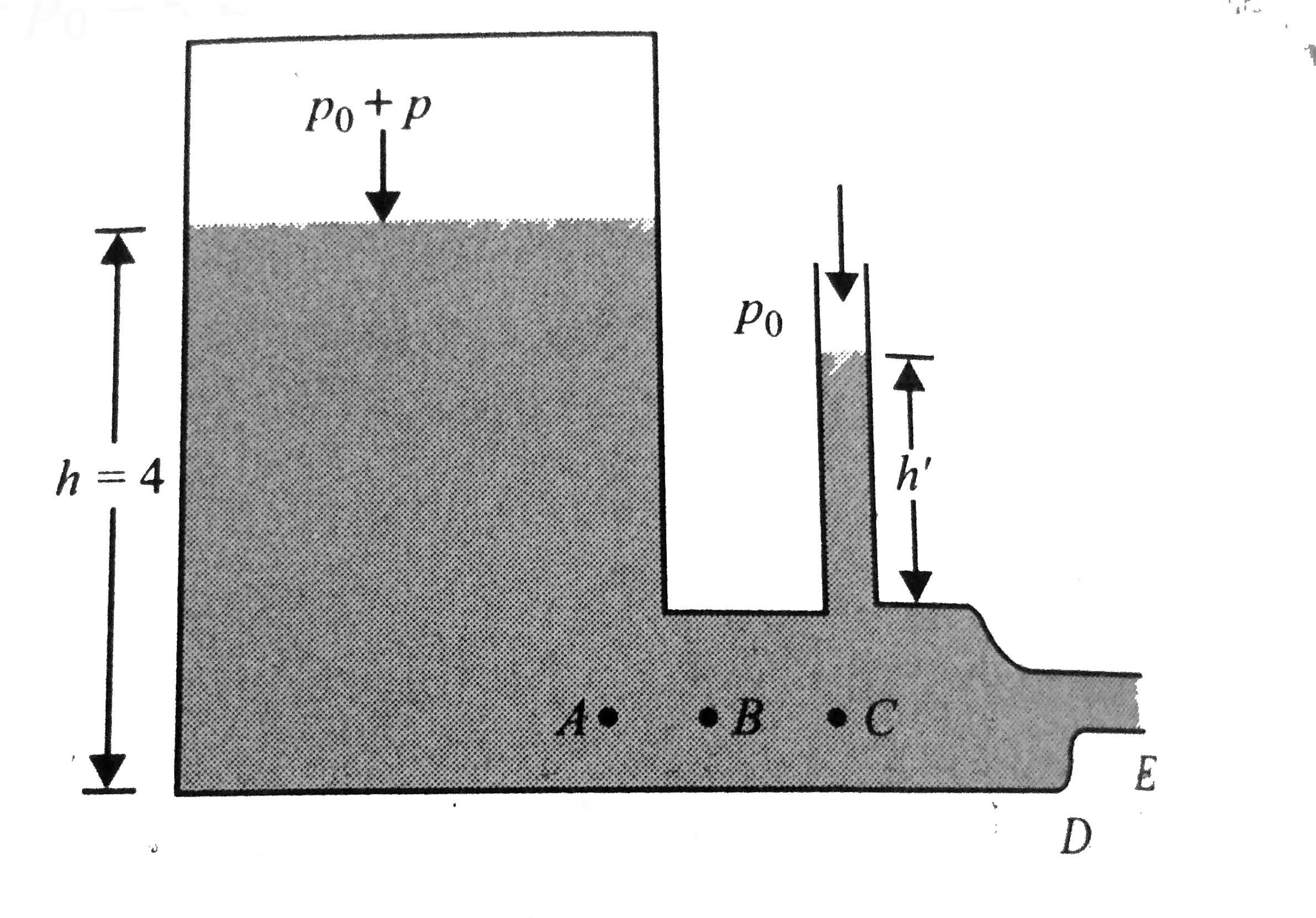
Pressure at $A, p_{A} = p + p_{0} + ρ g h$
From equation of continuity and Bernoulli's theorem,
$p_{B} = p_{C}$
Applying Bernoull's theorem at $A$ and $E$ , we have
$p + p_{0} + ρ g h = p_{c} + \frac{p v_{C}^{2}}{2} = p_{0} + \frac{p v_{E}^{2}}{2}$
where $v_{C}$ and $v_{E}$ are the velocities of flow of liquid at $C$ and $E$ , respectively.
From hydrostastics $p_{c} = p_{0} + ρ g h'$
From continuity equation $A_{C} v_{C} = A_{E} v_{E}$
Where $A_{C} = 6 c m^{2}$ and $A_{E} = 3 c m^{2}$
Solving above equation, we get $v_{E} = 13.4 m / s$
$v_{C} = 6.7 m / s$
$h' = 4.5 m$
Discharge rate
$Q = A_{E} v_{E} = 3 \times 10^{- 4} \times 13.4 m^{3} / s$
When a hole has been created at the top of the vessel, gange pressure drops to zero, i.e,, in above equation put $p = 0$ and get $h'$ .
$∴ h' = 3 m$

Updated on:21/07/2023

Class 11 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A liquid having density $6000 k g / m^{3}$ stands to a height of $4 m$ in a sealed tank as shown in the figure. The tank contains compressed air at a gauge pressure of $3 a t m$ . The horizontal outlet pipe has a cross-sectional area of $6 c m^{2}$ and $3 c m^{2}$ at larger and smaller sections. Atmospheric pressure $= 1 a t m, g = 10 m / s^{2} 1 a t m = 10^{5} N / m^{2}$ .

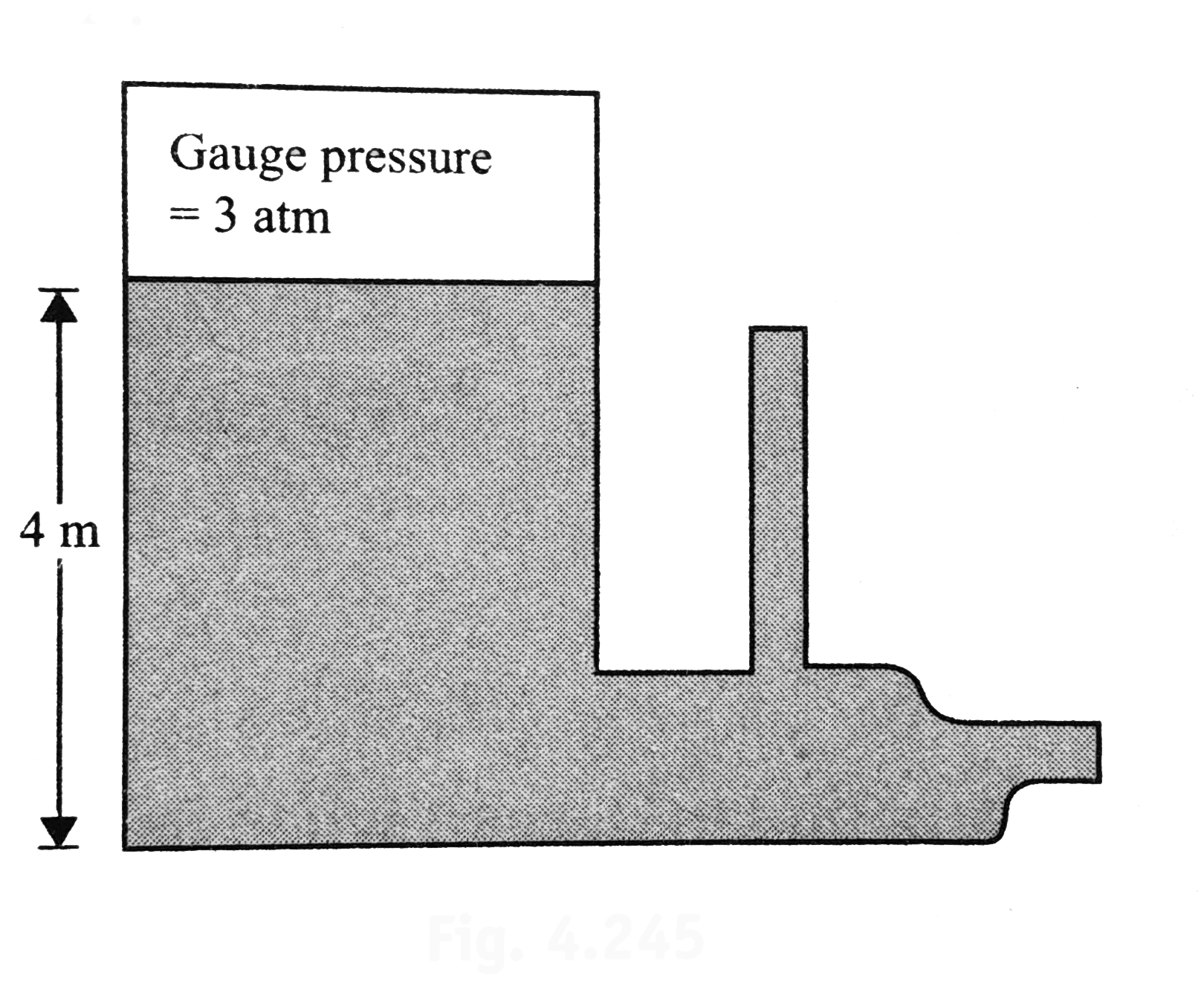
Assume that depth of water in the tank remains constant due to $s$ very large base and air pressure above it remains constant. Based on the above information, answer the following questions.
The height at which liquid will stand in the open end of the pipe is
A $4 m$
B $3.5 m$
C $4.5 m$
D $5.6 m$
Question 2 - Select One
A liquid having density $6000 k g / m^{3}$ stands to a height of $4 m$ in a sealed tank as shown in the figure. The tank contains compressed air at a gauge pressure of $3 a t m$ . The horizontal outlet pipe has a cross-sectional area of $6 c m^{2}$ and $3 c m^{2}$ at larger and smaller sections. Atmospheric pressure $= 1 a t m, g = 10 m / s^{2} 1 a t m = 10^{5} N / m^{2}$ .

Assume that depth of water in the tank remains constant due to $s$ very large base and air pressure above it remains constant. Based on the above information, answer the following questions.
The height at which liquid will stand in the open end of the pipe is
A $4 m$
B $3 m$
C $3.5 m$
D $3.8 m$
Question 3 - Select One or More

As shown in figure, a liquid of density $ρ$ is standing in sealed container to a height h. The container contains compressed air at a gauge pressure of p.The horizontal outlet pipe has a cross-sectional area A at C and D. The cross-sectional area is $A / 2$ at E. Find correct options:
AThe velocity of liquid at C will be ${[\frac{(P + ρ g h)}{4 ρ}]}^{1 / 2}$
BThe velocity of liquid at C will be ${[\frac{2 (P + ρ g h)}{ρ}]}^{1 / 2}$
Cthe discharge rate is given by $\frac{A}{2 ρ} {(p + ρ g h)}^{1 / 2}$
DThe discharge rate is given by $\frac{A}{2 \sqrt{ρ}} {(p + ρ g h)}^{1 / 2}$

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

As shown in figure, a liquid of density $ρ$ is standing in sealed container to a height h. The container contains compressed air at a gauge pressure of p.The horizontal outlet pipe has a cross-sectional area A at C and D. The cross-sectional area is $A / 2$ at E. Find correct options:

CENGAGE PHYSICS-FLUID MECHANICS-Linked Comprehension

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

As shown in figure, a liquid of density ρ is standing in sealed container to a height h. The container contains compressed air at a gauge pressure of p.The horizontal outlet pipe has a cross-sectional area A at C and D. The cross-sectional area is A/2 at E. Find correct options:

CENGAGE PHYSICS-FLUID MECHANICS-Linked Comprehension

As shown in figure, a liquid of density $ρ$ is standing in sealed container to a height h. The container contains compressed air at a gauge pressure of p.The horizontal outlet pipe has a cross-sectional area A at C and D. The cross-sectional area is $A / 2$ at E. Find correct options: