A liquid is coming out from a vertical tube. The relation between the weight of the drop W , surface tension of the liquid T and radius of the tube r is given by, if the angle of contact is zero
W=πr2T
W=2πrT
W=2r2πT
W=34πr3T
The correct Answer is:B
weight is balanced by force of surface tension.
∴w=2πrT
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
The liquid in the capillary tube will rise if the angle of contact is
View SolutionDue to capillary action, a liquid will rise in a tube, if the angle of contact is
View SolutionA liquid rises in a capillary tube when the angle of contact is:
View SolutionIf a capillary tube is dipped and the liquid levels inside and outside the tube are same. Then the angle of contact is
View SolutionThe correct curve between the height or depression h of liquid in a capillary tube and its radius is
View SolutionA liquid is contain in a vertical tube of semicircular cross section figure. The contact angle is zero. The force of surface tension on the curved part and on the flat part are in ratio

View SolutionTwo parallel glass plates are dipped partly in the liquid of density 'd' keeping them vertical. If the distance between the plates is 'x', Surface tension is T and angle of contact is θ then rise of liquid between the plates due to capillary will be
View Solution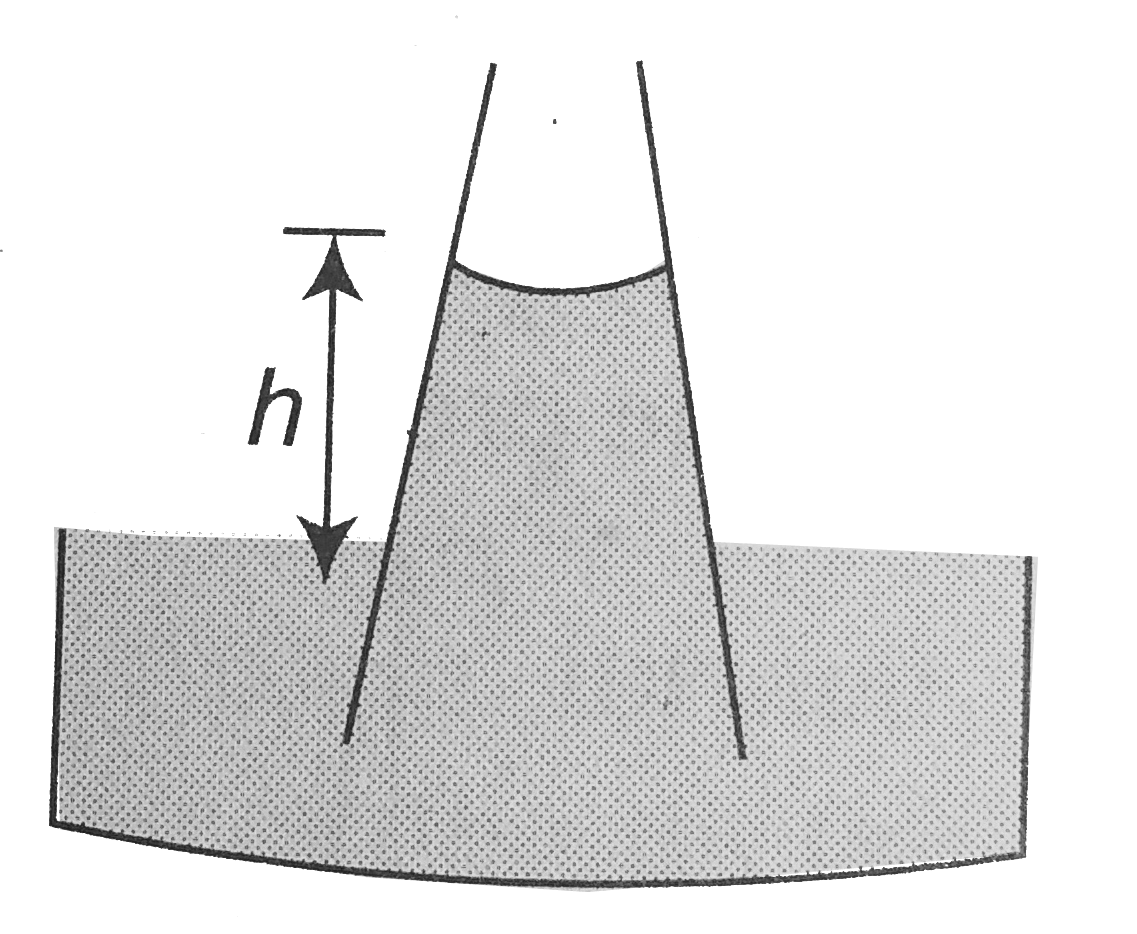
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:
View SolutionA : The apparent weight of a body floating on the surface of a liquid is zero.
R : The net force on a body floating on the surface of a liquid is zero.
View SolutionA student writes the equation for the capillary rise of a liquid in a tube as h=ρg2Tcosθ, where r is the radius of the capillary tube, ρ is the density of liquid, T is the surface tension and θ is the angle of contact. Check the correctness of the equation using dimensional analysis?
View Solution
