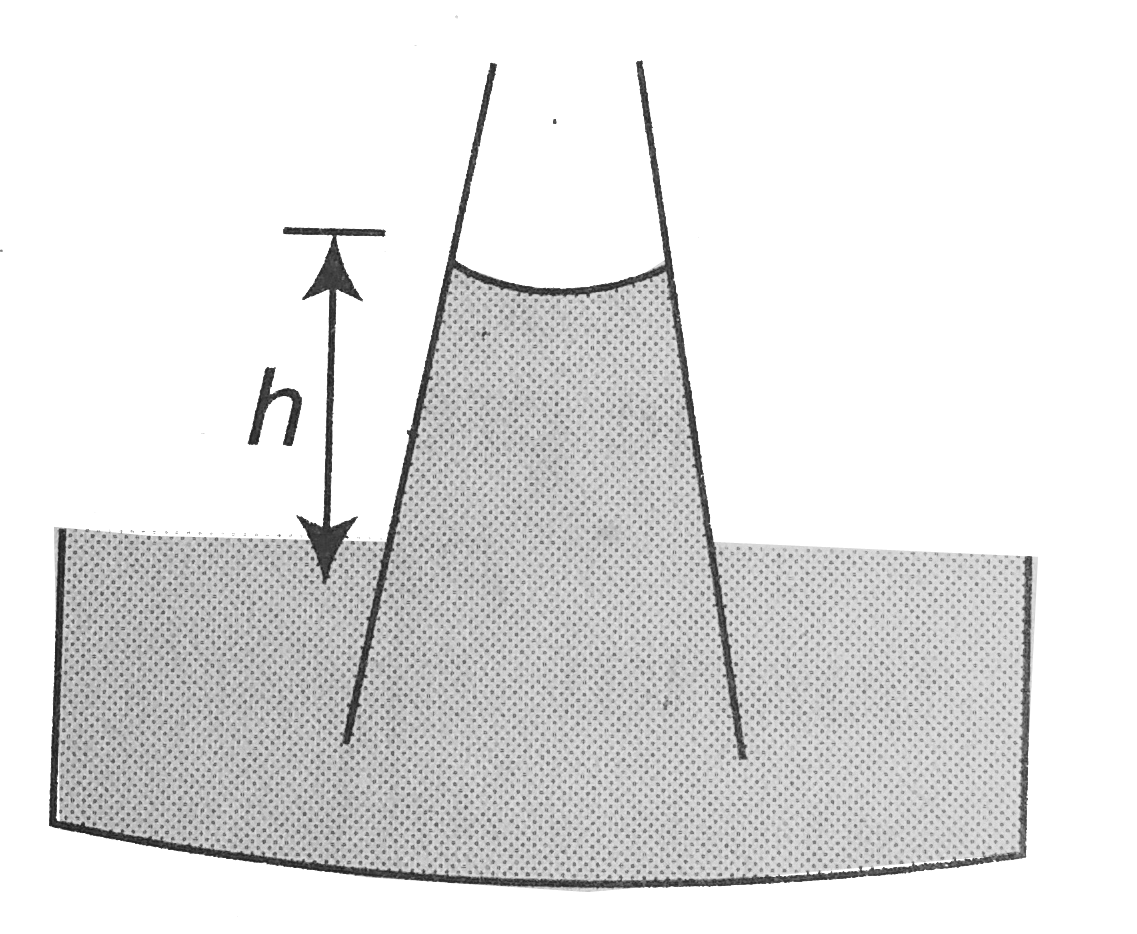
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is $0^{\circ}$ and effect of liquid inside the mexiscus is to be neglected. $T$ is surface tension of the liquid, $r$ is radius of the meniscus, $g$ is acceleration due to gravity and $ρ$ is density of the liquid then height $h$ in equilibrium is:

greater than $\frac{2 T}{r ρ g}$

equal to $\frac{2 T}{r ρ g}$

less than $\frac{2 T}{r ρ g}$

of any value depending upon actual value

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Answer

Step by step video & image solution for A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0^@ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and rho is density of the liquid then height h in equilibrium is: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A capillary tube is taken from the Earth to the surface of the moon. The rise of the liquid column on the Moon (acceleration due to gravity on the Earth is 6 times that of the Moon) is
Asix times that on the earth's surface
B1/6 that on tha earth surface
Cequal on that of the earth surface
Dzero
Question 2 - Select One
The radii of the two columne is U-tube are $r_{1}$ and $r_{2} (> r_{1})$ . When a liquid of density $ρ$ (angle of contact is $0^{\circ}))$ is filled in it, the level different of liquid in two arms is h. The surface tension of liquid is
$(g =$ acceleration due to gravity)
A $\frac{ρ g h r_{1} r_{2}}{2 (r_{2} - r_{1})}$
B $\frac{ρ g h (r_{1} - r_{2})}{2 r_{1} r_{2}}$
C $\frac{2 (r_{2} - r_{1})}{ρ g h r_{1} r_{2}}$
D $\frac{ρ g h}{2 (r_{2} - r_{1})}$

ALLEN-ELASTICITY, SURFACE TENSION AND FLUID MECHANICS-Exercise 2 (One or more than one correct answer)

Home
Ask Doubt
Profile

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

A capillary tube is taken from the Earth to the surface of the moon. The rise of the liquid column on the Moon (acceleration due to gravity on the Earth is 6 times that of the Moon) is

The radii of the two columne is U-tube are r1 and r2(>r1). When a liquid of density ρ (angle of contact is 0∘)) is filled in it, the level different of liquid in two arms is h. The surface tension of liquid is (g= acceleration due to gravity)

ALLEN-ELASTICITY, SURFACE TENSION AND FLUID MECHANICS-Exercise 2 (One or more than one correct answer)

The radii of the two columne is U-tube are $r_{1}$ and $r_{2} (> r_{1})$ . When a liquid of density $ρ$ (angle of contact is $0^{\circ}))$ is filled in it, the level different of liquid in two arms is h. The surface tension of liquid is
$(g =$ acceleration due to gravity)