A liquid of density ρ is in a bucket that spins with angular velocity 'ω' as shown in figure. Prove that the free surface of the liquid has a parabolic shape. Find equation of this.
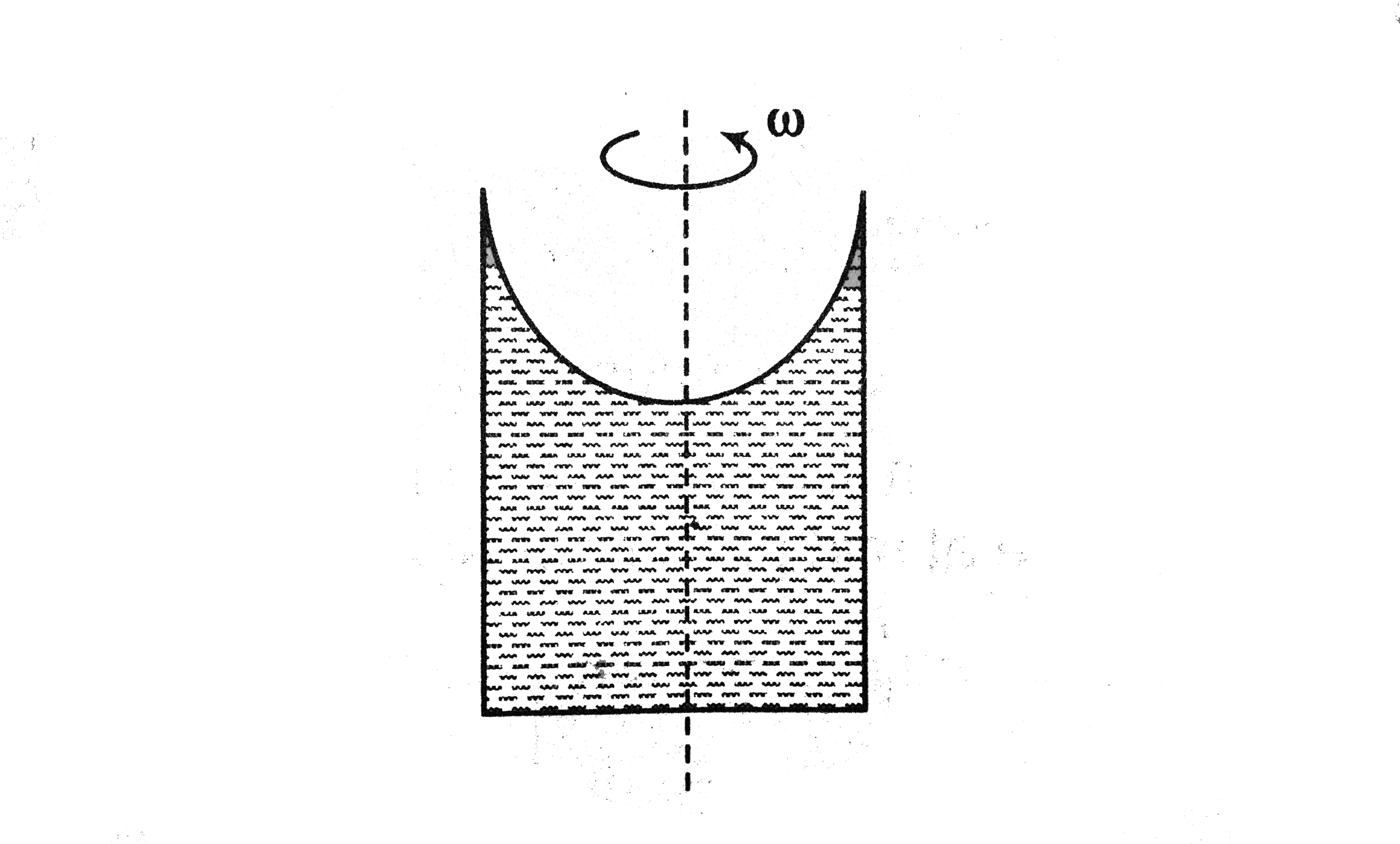 .
.
The correct Answer is:A
In the figure shown, suppose the coordinates of point M are (x,y) with respect to the coordinates axes.

Then, MN=y,NQ=x
Points M and Q are open to atmosphere.
∴pM=pQ=atmosphric pressure p_(0)<br>Now,pM−pN=−ρgy
⇒p0−pN=−ρgy ...(i)
pN−pQ=ρω2x22
∴pN−p0=ρω2x22...(ii)
Adding Eqs. (i) and (ii), we have
0=−ρgy+ρω2x22
y=ω2x22g
This is required equation of free surface of the liquid and we can see that this is an equation of a parabola.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples21videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Miscellaneous Examples10videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
A liquid of density 'ρ' is rotated with an angular speed 'ω' as shown in figure. Using the pressure equation concept find the equation of free surface of the liquid.
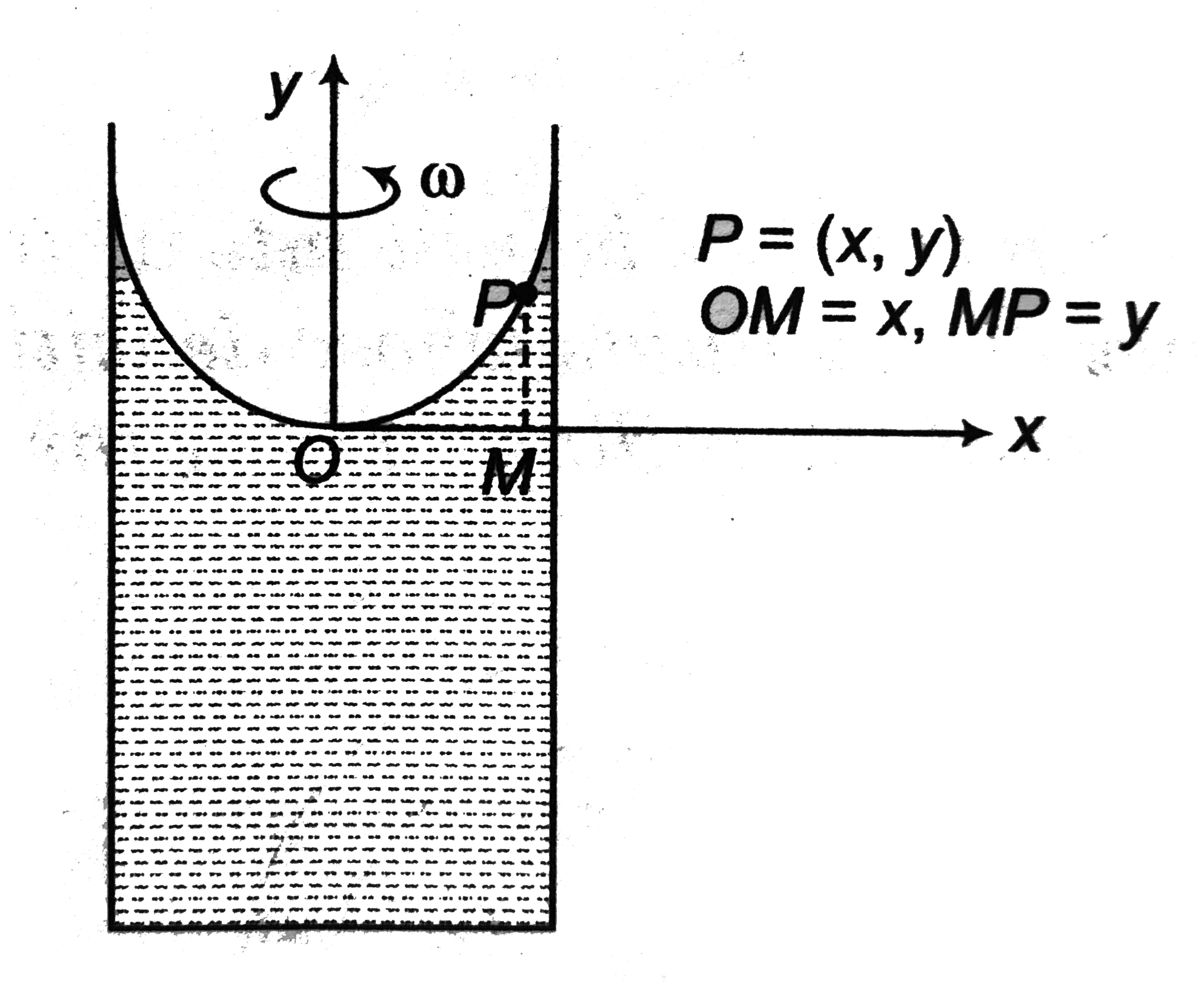 .View Solution
.View SolutionA body of mass m and radius r is rotated with angular velocity ω as shown in the figure & kept on a surface that has sufficient friction then the body will move
 View Solution
View Solution
A liquid of density ρ is rotated by an angular speed ω as shown in figure,Using the concept of pressure equation, find a relation between h1,h2,x1 and x2.View SolutionA liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
View SolutionA non viscous liquid of density ρ is filled in a tube with A as the area of cross section, as shown in the figure. If the liquid is slightly depressed in one of the arms, the liquid column oscillates with a frequency
 View Solution
View SolutionDensity of a liquid varies with depth as ρ=αh. A small ball of density ρ0 is released from the free surface of the liquid. Then
View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
View SolutionEqual volumes of two immiscible liquids of densities ρand2ρ are filled in a vessel as shown in figure. Two small holes are punched at depth h/2 and 3h/2 from the surface of lighter liquid. If v1andv2 are the velocities of efflux at these two holes then (v2v1)2 is
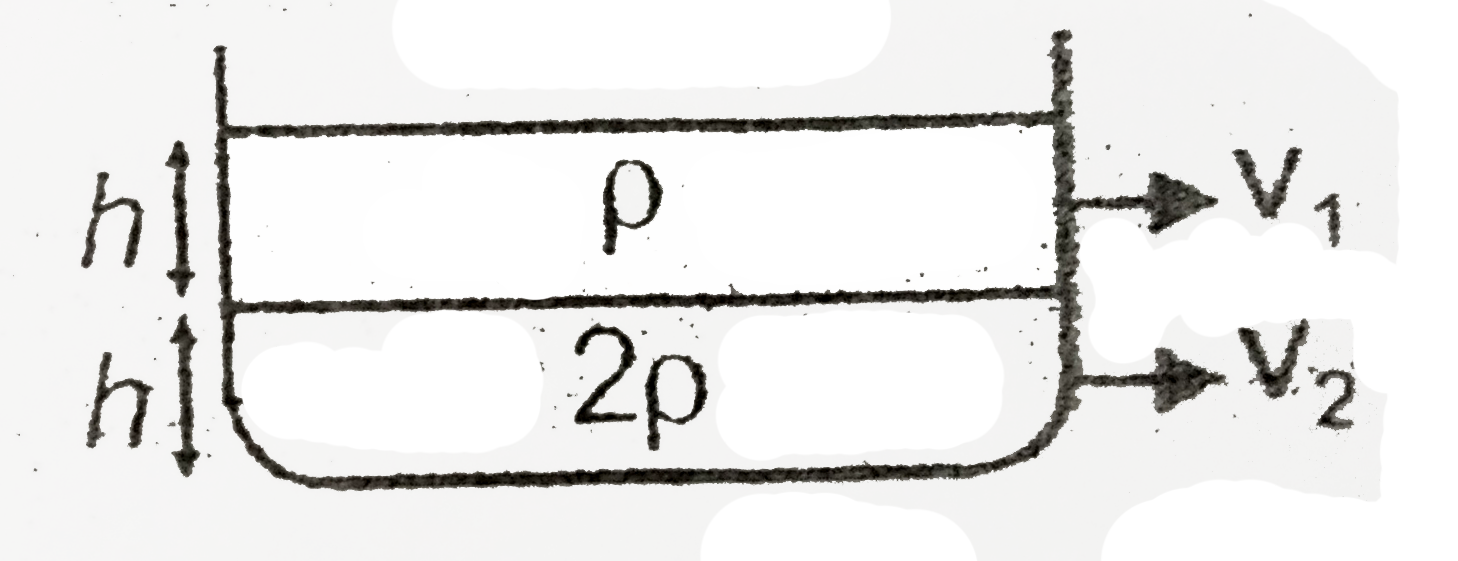 View Solution
View SolutionIn a U-tube, two immiscible liquids of density ρ1andρ2 are arranged as shown in figure. The right part of the tube is closed at the top and some air is entrapped above liquid of density ρ2. The gauge pressure of this air is :
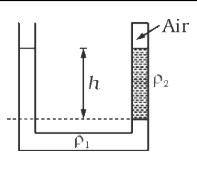 View Solution
View SolutionA liquid of density ρ has to spray with help of aspirator pump at height H from liquid level as shown in figure. If gauge pressure inside bulb is P and density of air is σ then velocity of air in tube AB is
 View Solution
View Solution

