A liquid of mss m is set into oscillations in a U-tube of cross section A. Its time period recorded is T, where T=2π√l/2g , here l is the length of liquid column. If the liquid of same mass is set into oscillations in U-tube of cross-section A/16 then determine time period of oscillation.
As mass is constant
∴ Volumn x density =constant (∵ Density=MassVolumn)
⇒V1d=V2d
where , V1 and V2 are the volumn of liquid in U-tube in two cases respectively
(Al)d=∣∣∣A16l'∣∣∣dimpliesl'=16l
∵T=2π√12g
∴T'T=√l'l=√16ll=4⇒T'=4T
Similar Questions
A liquid of mass m set into oscillations in a U-tube of cross section A. Its time period recorded is T, where T=2π√l2g, here l is the length of liquid column. If the liquid of same mass is set into oscillaions in U-tube of cross section A16 then determine time period of oscillation.
View SolutionFind time period of liquid column of length l in the shown tube.

View Solution
Knowledge Check
A uniform rod of length 2.0 m is suspended through an end and is set into oscillation with small amplitude under gravity. The time period of oscillation is approximately
A1.60secB1.80 secC2.0 secD2.40 secA particle of mass m is executing oscillations about the origin on the x-axis, it's potential energy is U(x)=k|x|2, where k is a positive constant, if the amplitude of oscillation is a, then it's time period T is
AProportional o1√aBIndependent of aCProportional to √aDProportional to a3/2A spring elongated by length 'L' when a mass 'M' is suspended to it. Now a tiny mass 'm' is attached and then released, its time period of oscillation is -
A2π√(M+m)lMgB2π√mlMgC2π√L/gD2π√Ml(m+M)g
The time period of an oscillating body is given by T=2π√madg. What is the force equation for this body?
View SolutionA simple pendulum of length l0 can perform simple harmonic oscillations with a time period T0. If the length of the pendulum is decreased to l016 then the time time period of oscillation will become.
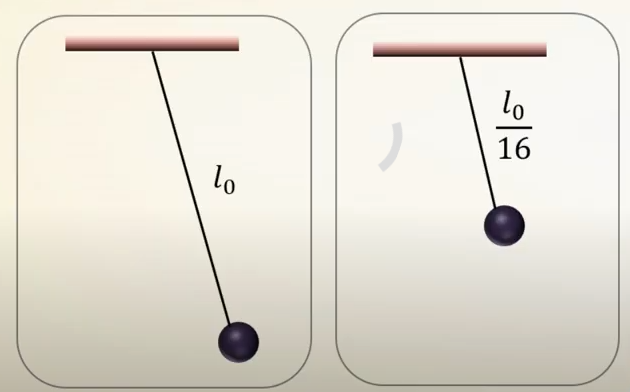
View SolutionA vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
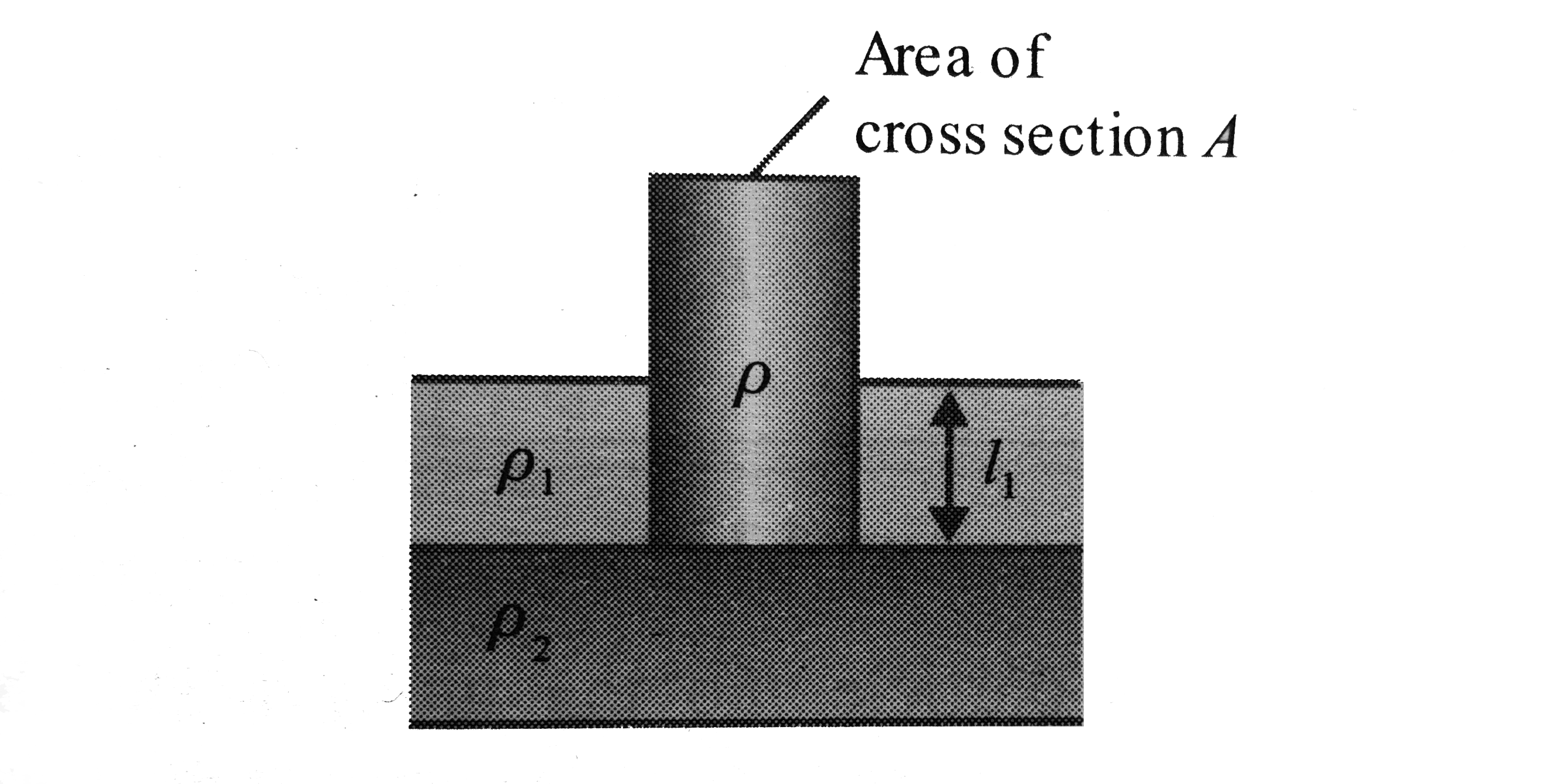
View SolutionA simple pendulum of length l is made to oscillate with an amplitude of 45 degrees. The acceleration due to gravity is g. Let T0=2π√l/g . The time period of oscillation of this pendulum will be -
View SolutionA test tube of length l and area of cross-section A has some iron fillings of mass M. The test tube floats normally in a liquid of density ρ with length x dipped in the liquid. A distribuing force makes the tube oscillate in the liquid. The time period of osciallation is given by (neglect the mass of the test tube)
View Solution
