A load of 10kN is supported from a pulley which in turn is supported by a rope of sectional area 1×103mm2 and modulus of elasticity 103Nmm−2, as shown in figure. Neglecting the friction at the pulley, determine the deflection of the load.
Let T be the tension in the rope. Then
2T=10kN⇒T=5N

Hence longitudinal stress in the rope is
σ=TA=5kN103mm2=5N/mm2
Extension in the rope =StressY×L
=−5N/mm2103N/mm×1500mm=7.5mm
Therefore, deflection of the load δ=7.52=3.75mm
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Solved Examples
11 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.1
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Video
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
The figure shows two creates that are connected by a steel wire that passes over a pulley. The unstretched length of the wire is 1.5 m, and its cross - sectional area is 1.3×10−5m2. The pulley is frictionless and massless. When the crates are accelerating, determine the change in length of the wire. Ignore the mass of the wire.
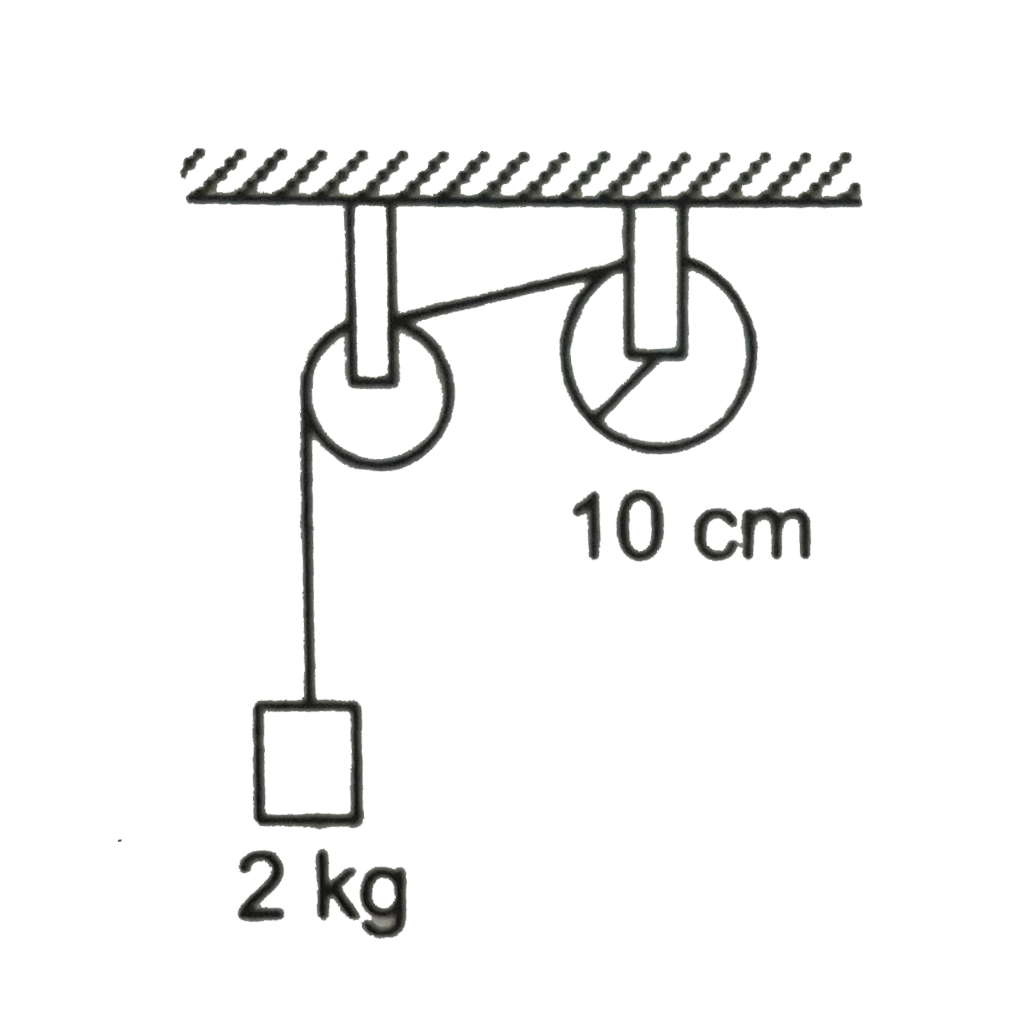
View SolutionA string is wrapped on a wheel of moment of inertia 0.20 kg-m^2 and radius 10 cm and goes through a light pulley to support a block of mas 2.0 kg as shown in figure. Find the acceleration of the block.
View Solution
Knowledge Check
A load of 10KN is supported from a pulley , which in turn is supported by a rope of cross-sectional area 103mm2 and modulus of elasticity 103Nmm−2 as shown in the figure. Neglecting friction at the pulley , then downward deflection of the load (in mm) is
 A3.75B4.25C2.75D4.00
A3.75B4.25C2.75D4.00The axle of a pulley of mass 1kg is attached to the end of an elastic string of length 1m, cross- sectional area 10−3m2 and young's modulus 2×105Nm−2,whose other end is fixed to the ceiling. A rope of negligible mass is placed on the pulley such that its left end is fixed to the ground and its right end is hanging freely , from the pulley which is at rest in equilibrium . Now, the rope and the pulley can be neglected. (Given, g=10ms−2)

The elongation of the string before applying force isA50cmB5cmC0.5cmD0.05cmA load of 1kg weight is attacheed to one end of a steel wire of cross sectional area 3mm2 and Young's modulus 1011N/m2. The other end is suspended vertically form a hook on a wall, then load is pulled horizonatally and relased. When the load passes through its lowest position the fractional change in length is (g=10m/s2)
A10−4B10−3C103D104
The force in newton required to increase by 1% length of a rod of area of cross section 10−3m squre is …….., Modulus of elaticity of rod is 1.2×1012Nm−2
View SolutionA uniform bar of length 2 m and cross-sectional area 50cm2 is subjected to a tensile load 100 N. If Young's modulus of material of bar is 2×107N/m2 and poisson's ratio is 0.4, then determine the volumetric strain.
View SolutionA stress of 1kg/mm2 is applied on a wire. If the modulus of elasticity of the wire is 1010dyne/cm2, then the percentage increase in the length of the wire will be
View SolutionEach of three blocks shows in figure has a mass 3 kg. The wire connecting blocks A and B has area of cross-section 0.005cm2 and Young's modulus of elasticity Y=2×1011N/m2 . Neglect friction. Find the elasticity potential energy stored per unit volume in wire connecting blocks A and B in steady state.
(Takeng=10m/s2)
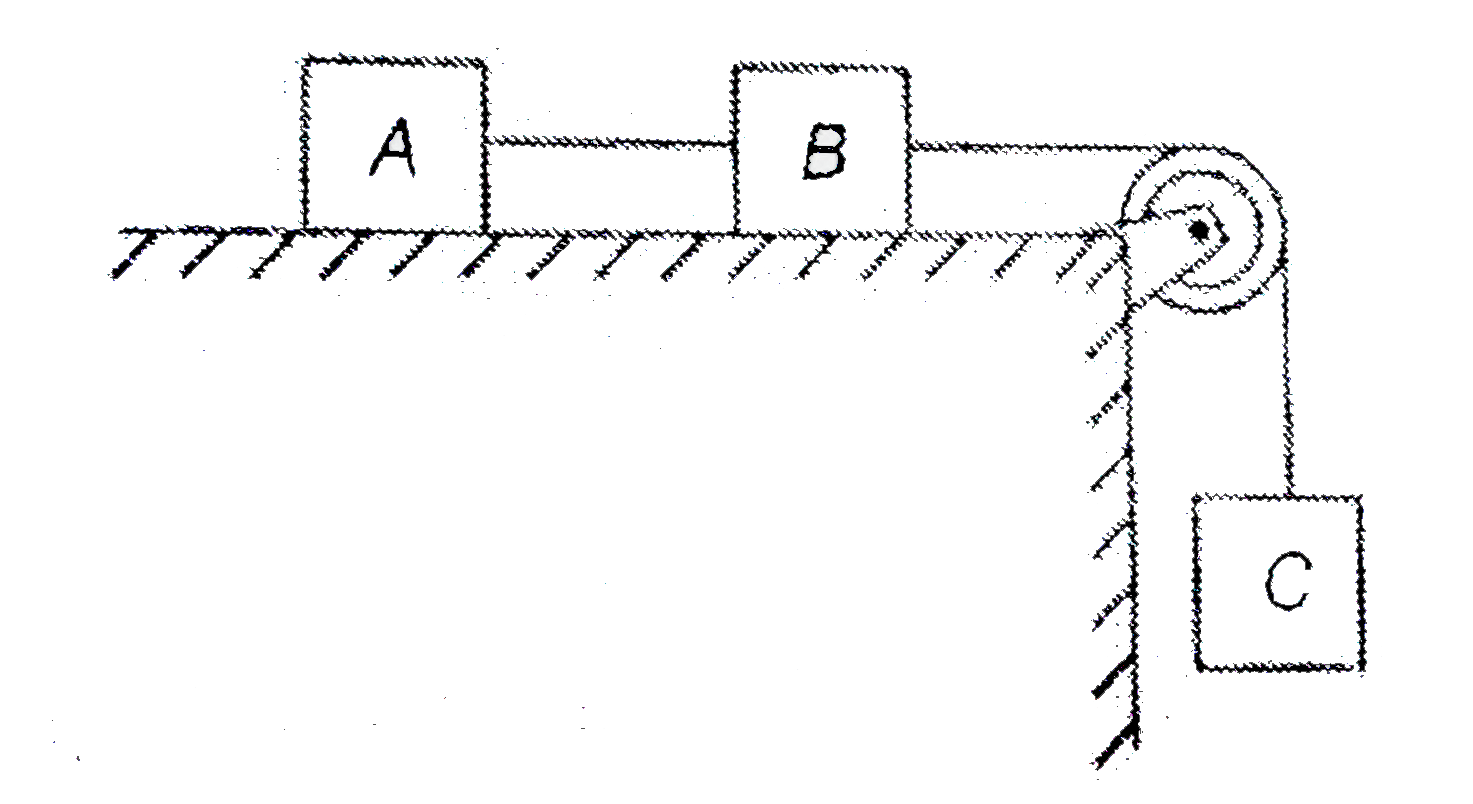
View SolutionA load o f 1 kg weight is a attached to one end of a steel wire o f area of cross-section 3mm2 and Young's modulus 1011N/m2 . The other end is suspended vertically from a hook on a wall , then the load is pulled horizontally and released .When the load passes through its lowest position the fraction al change in lenght is (Takeg=10m/s2)
View Solution