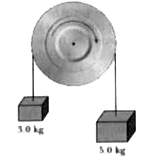
The figure shows two creates that are connected by a steel wire that passes over a pulley. The unstretched length of the wire is 1.5 m, and its cross - sectional area is 1.3×10−5m2. The pulley is frictionless and massless. When the crates are accelerating, determine the change in length of the wire. Ignore the mass of the wire.
4.3×10−5m
3.2×10−5m
2.1×10−5m
2.5×10−6m
The correct Answer is:C
Step by step video & image solution for The figure shows two creates that are connected by a steel wire that passes over a pulley. The unstretched length of the wire is 1.5 m, and its cross - sectional area is 1.3xx10^(-5)m^(2). The pulley is frictionless and massless. When the crates are accelerating, determine the change in length of the wire. Ignore the mass of the wire. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
8 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)
6 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - CHECKPOINT
1 Videos
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Integer Type)
3 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )
3 Videos
Similar Questions
Compute the elongation of the steel wire in the figure. Unloaded length of the steel wire =1.5 m, the diameter of the wire is 0.25 m, Young's modulus of steel is 2×1011 N m−2.
View SolutionA current of 3 A is flowing through a wire of length 2 m and cross- sectional area 1mm2. If wire contains 1029electrons/m3, calculate the average time taken by an electron to cross the length of the wire.
View Solution
Knowledge Check
In CGS system, the Young's modulusm of a steel wire is 2×1012. To double the length of a wire of unit cross-section area, the force
A4×106 dynesB2×1012 dynesC2×1012 newtonsD2×108 dynesTwo particles of masses m and M(M>m) are connected by a cord that passes over a massless, frictionless pulley. The tension T in the string and the acceleration a of the particles is
AT=2mM(M−m)g,aMm(M+m)gBT=2mM(M+m)g,a=(M−mM+m)gCT=(M−mM+m)g,a=(2mM(M+m))gDT=(Mm(M+m)g,a=(2mM(M+m))gThe Young's modulus of a wire of length 2m and area of cross section 1mm2 is 2×1011N/m2. The work done in increasing its length by 2mm is
A0.1 JB0.2 JC0.02 JD0.4 J
Two blocks of masses m and M are connected by means of a metal wire passing over a frictionless fixed pulley. The area of cross-section of the wire is 6.5×10−9m2 and its breaking stress is 2×109Nm−2. If m = 1kg, then calculate the maximum value of M (g=10m/s2)
View SolutionCalculate the force required to increase the length of a steel wire of cross- sectional area 10−6m2 by 0.5% given: Y(for steel)=2×1011N−m2
View SolutionTwo block of mass m and M are connected means of a metal of a metal wire passing over a frictionless fixed pulley. The area of cross section of the wire is 6.67×10−9m2 and its breaking stress is 2×109Nm−2. If m = 1kg. Find the maximum value of M in kg for which the wire will not break. (g=10m/s2).
View SolutionWhen a resistance wire is passed through a die the cross-section area decreases by 1%, the change in resistance of the wire is
View SolutionTwo blocks of masses m and 2m are connected through a wire fo breakig stress S passing over a frictionless pulley. The maximum radius of the wire to be used so that the wire may not break is
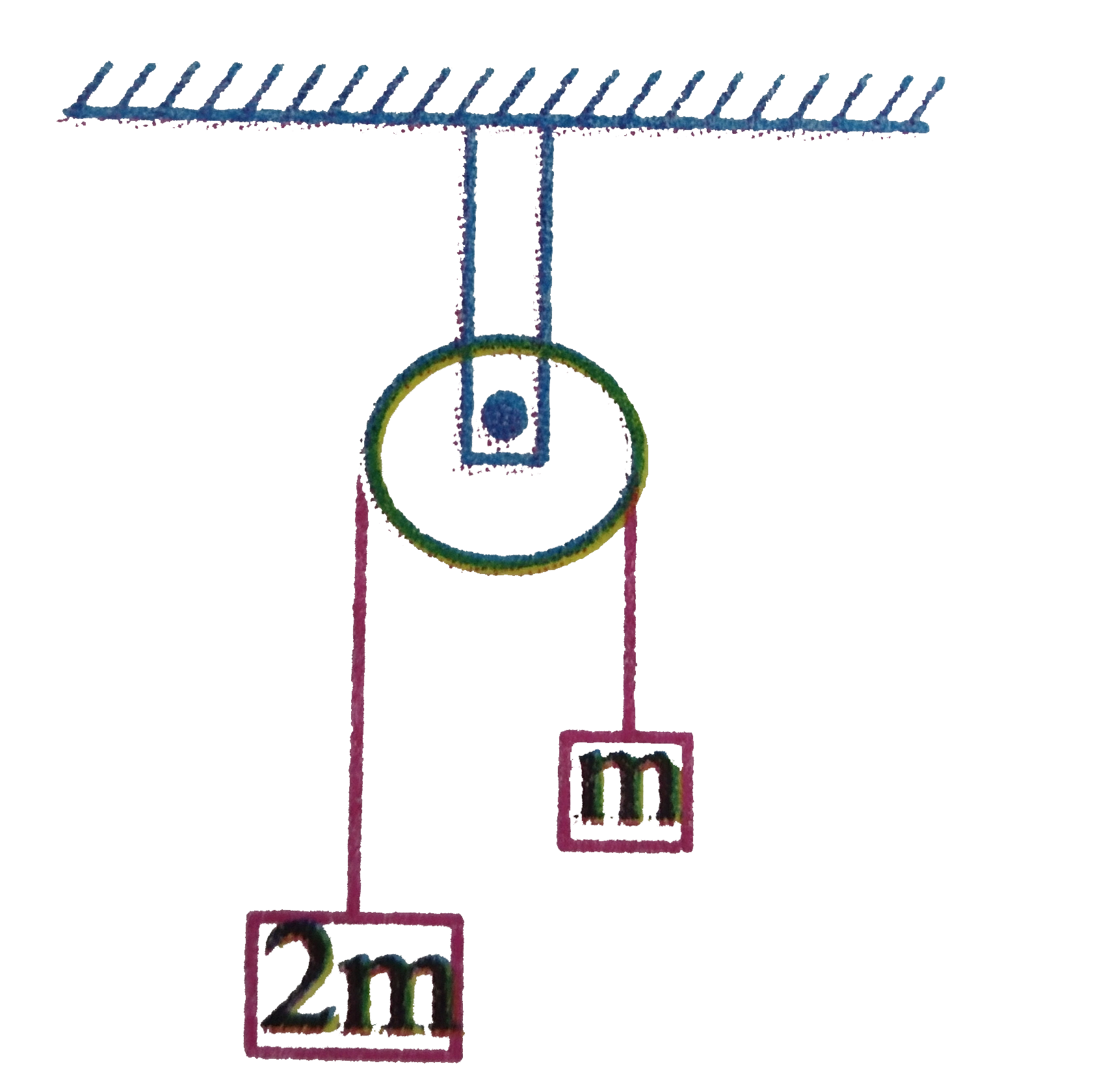
View Solution
