A long conducting wire of radius 1 cm carrying current of 1 A placed with its axis coinciding with X-axis. Find the magnetic field at point having coordinates (0.5cm,0.5cm) .
The correct Answer is:1×10−5T
To find the magnetic field at the point (0.5 cm, 0.5 cm) due to a long conducting wire carrying a current of 1 A, we can use Ampere's Circuital Law. Let's go through the solution step by step.
Step 1: Understand the Geometry
The wire is a long straight conductor with its axis along the x-axis. The radius of the wire is 1 cm. The point where we need to find the magnetic field has coordinates (0.5 cm, 0.5 cm), which means it is located in the xy-plane.
Hint: Visualize the wire and the point in a coordinate system to understand their positions relative to each other.
Step 2: Determine the Distance from the Wire
The point (0.5 cm, 0.5 cm) is at a distance from the wire. The distance r from the center of the wire to the point can be calculated using the Pythagorean theorem:
r=√(0.5)2+(0.5)2=√0.25+0.25=√0.5 cm=0.707 cm
Hint: Use the Pythagorean theorem to find the distance from the wire to the point.
Step 3: Apply Ampere's Circuital Law
According to Ampere's Circuital Law:
∮B⋅dL=μ0Ienclosed
For a circular path around the wire, the magnetic field B is constant along the path, so we can simplify the left side:
B⋅(2πr)=μ0Ienclosed
Hint: Remember that Ienclosed is the current enclosed by the path. For a point outside the wire, the enclosed current is the total current flowing through the wire.
Step 4: Calculate the Enclosed Current
Since the point is outside the wire, the enclosed current Ienclosed is simply the total current flowing through the wire, which is given as 1 A.
Hint: Identify that the current flowing through the wire is the same as the enclosed current when the point is outside the wire.
Step 5: Substitute Values into the Equation
Now we can substitute the values into the equation:
B⋅(2π⋅0.707×10−2)=μ0⋅1
Where μ0=4π×10−7T m/A.
Hint: Make sure to convert all units to SI units for consistency.
Step 6: Solve for B
Rearranging the equation gives:
B=μ0⋅12π⋅0.707×10−2
Substituting the value of μ0:
B=4π×10−72π⋅0.707×10−2=2×10−70.707×10−2=2×10−50.707≈2.83×10−5T
Hint: When simplifying, ensure to keep track of the powers of ten and the constants.
Final Answer
The magnetic field at the point (0.5 cm, 0.5 cm) is approximately 2.83×10−5T.
The wire is a long straight conductor with its axis along the x-axis. The radius of the wire is 1 cm. The point where we need to find the magnetic field has coordinates (0.5 cm, 0.5 cm), which means it is located in the xy-plane.
The point (0.5 cm, 0.5 cm) is at a distance from the wire. The distance r from the center of the wire to the point can be calculated using the Pythagorean theorem:
r=√(0.5)2+(0.5)2=√0.25+0.25=√0.5 cm=0.707 cm
According to Ampere's Circuital Law:
∮B⋅dL=μ0Ienclosed
For a circular path around the wire, the magnetic field B is constant along the path, so we can simplify the left side:
B⋅(2πr)=μ0Ienclosed
Since the point is outside the wire, the enclosed current Ienclosed is simply the total current flowing through the wire, which is given as 1 A.
Now we can substitute the values into the equation:
B⋅(2π⋅0.707×10−2)=μ0⋅1
Where μ0=4π×10−7T m/A.
Rearranging the equation gives:
B=μ0⋅12π⋅0.707×10−2
Substituting the value of μ0:
B=4π×10−72π⋅0.707×10−2=2×10−70.707×10−2=2×10−50.707≈2.83×10−5T
The magnetic field at the point (0.5 cm, 0.5 cm) is approximately 2.83×10−5T.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Conceptual Questions
29 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Tough & Tricky (PROBLEMS )
15 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - CHAPTER PRACTICE TEST
13 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
A long conducting wire of radius 5 cm, carrying current of 2 A is placed with its axis coinciding with Y-axis and lies on XZ-plane. Calculate the magnetic field induction at point A (3 cm, 3 cm, 3 cm) and (8 cm, 8 cm, 8 cm) if relative magnetic permeability of conductor is 300.
View SolutionA circular coil of radius 1⋅5cmcarriesacurrentof1⋅5A. If the coil has 25 turns , find the magnetic field at the centre.
View Solution
Knowledge Check
An 8 cm long wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. If the magnetic field inside the solenoid is 0.3 T, then magnetic force on the wire is
A0.14NB0.24NC0.34ND0.44NA long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field →B at a point having coordinnates (x, y) in the z = 0 plane is
Aμ0I(yˆi−xˆj)2π(x2+y2)Bμ0I(xˆi+yˆj)2π(x2+y2)Cμ0I(xˆj−yˆi)2π(x2+y2)Dμ0I(xˆi−yˆj)2π(x2+y2)
A long straight wire carrying current i=10A lies along y-axis. Find the magnetic field at P(3cm, 2cm,4cm).

View SolutionA current of 10A is established in a long wire along the positive z-axis. Find the magnetic field (vec B) at the point (1m , 0 , 0).
View SolutionA solid wire of radius 10 cm carries a current of 5.0 A distributed uniformly over its cross section. Find the magnetic field B at a point at a distance (a) 2 cm (b) 10 cm and (c) 20 cm away from the axis. Sketch a graph of B versus x for 0ltxlt20 cm .
View SolutionA long straight solid conductor of radius 6cm carries a current of 8A, which uniformly distributed over its circular cross-section. Find the magnetic field (a) at a distance of 3cm from the axis of the conductor (b) at a distance 10cm from the axis of the conductor.
View SolutionA circular coil, having 100 turns of wire of radius (nearly) 20 cm each, lies in the X-Y plane with its centre at the origin of coordinates. Find the magnetic field at the point (0,0,20√3cm), when the coil carries a current of (2π) A.
View Solution(a) Find the magnetic field at the point O if the wire carrying a current i has the shape shown. The radius of the current part of the wire is R, the linear parts of the wire are very long.
(i)
(ii)
(iii)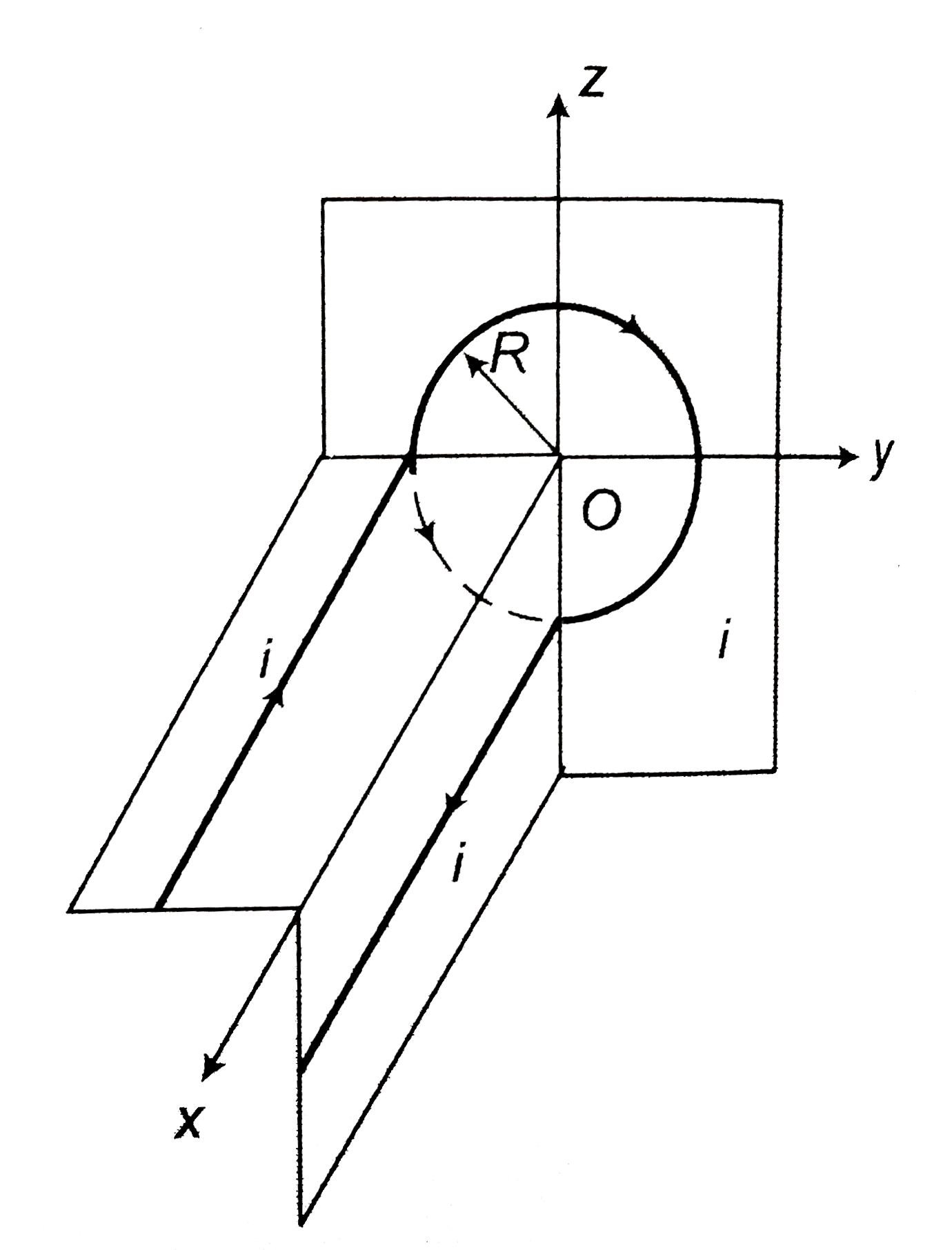
(b) A long straight wire along the z-axis carriers a current i in negative z-direction. Find magnetic field in vector from at a point having co-ordinates (x,y) on z=0 plane.
(c) A non-coplaner loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop of length 2a. find unit vector along magnetic field magnetic filed at the point P(a,0,a).
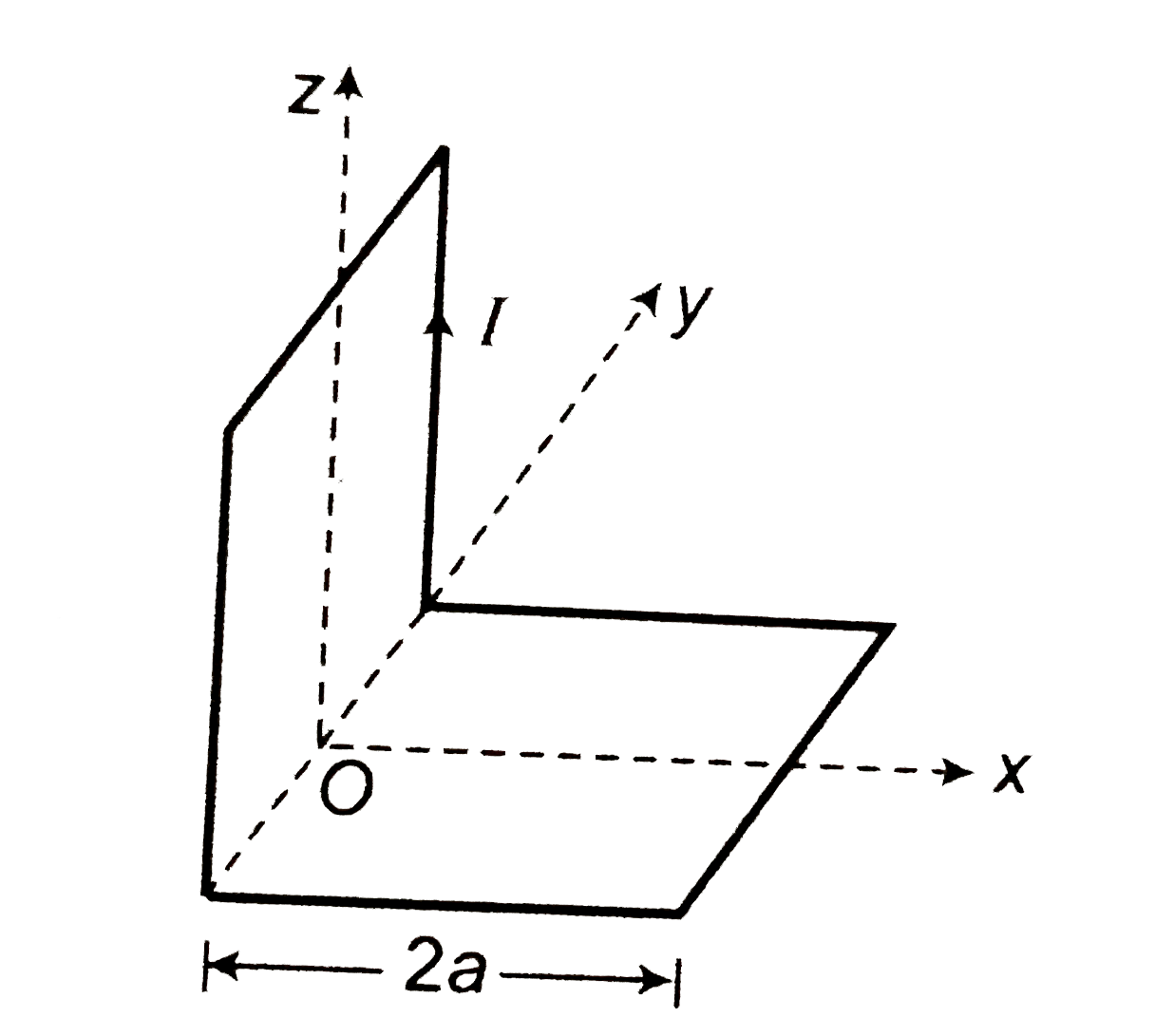
View Solution
