A long straight cable of length l is placed symmetrically along z-axis and has radius a(<<l). The cable consists of a thin wire and a co- axial conducting tube. An alternating current I(t)=I0 sin (2πvt). Flows down the central thin wire and returns along the co-axial conducting tube. the induced electric at a distance s from the wire inside the cable is
E(s,t)=μ0I0v cos (2πvt)In(sa)ˆk.
(i) Calculate the displacement current density inside the cable.
(ii) Integrate the displacement current density across the cross- section of the cable to find the total displacement current Id.
(iii) compare the conduction current I0 with the displacement current Id0.
(i) Given, the induced electric field at a distance r from the wire inside the cable is
→E(s,t)=μ0I0vcos(2πvt)loge(sa)ˆk
Displacement current density,
→JD=∈0−→dEdt=∈0ddt[μ0I0vcos(2πvt)loge(sa)ˆk]
=∈0μ0I0vddt[cos2πvt]loge(sa)ˆk=1c2I0v22π[−sin2πvt]loee(sa)ˆk
=v2c22πI0sin2πvtloge(as)ˆk[∵loge(sa)=−loge(as)]
=1λ22πI0loge(as)sin2πvtˆk=2πI0λ2logeassin2πvtˆk
(ii) ID=∫JDsdsdθ=∫as=0∫2π0dθ=∫as=0JDsds×2π
=∫a0[2πλ2I0loge(as)sdssin2πvt]×2π=(2πλ)2I0∫as=0loge(as)sdssin2πvt
(2πλ)2I0∫as=0loge(as)12d(s2).sin2πvt=a22(2πλ)2I0sin2πvt∫as=0loge(as).d(sa)2
a24(2πλ)2I0sin2πvt∫as=0loge(as).d(sa)2=−a24(2πλ)2I0sin2πvt∫as=0loge(as).d(sa)2
=−a24(2πλ)2I0sin2πvt×(−1)[∵∫as=0loge(as).d(sa)2=−1]
ID=a24(2πλ)2I0sin2πvt=(2πa2λ)2I0sin2πvt
(iii) The diplacement current, ID=(2πa2λ)2I0sin2πvt=I0Dsin2πvt
where I0D=(2πa2λ)2I0=(πaλ)2I0∴I0DI0=(aπλ)2
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Higher order Thinking skills2videos
ELECTROMAGNETIC WAVES
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Value based questions5videos
ELECTROMAGNETIC WAVES
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - short answer question2videos
ELECTROMAGNETIC WAVES
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Multiple Choice Questions1videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks1videos
ELECTRONIC DEVICES
Similar Questions
A long straight cable of length l is placed symmetrically along z-axis and has radius a(<<l). The cable consists of a thin wire and a co- axial conducting tube. An alternating current I(t)=I0 sin (2πvt). Flows down the central thin wire and returns along the co-axial conducting tube. the induced electric at a distance s from the wire inside the cable is
E(s,t)=μ0I0v cos (2πvt)In(sa)ˆk.
(i) Calculate the displacement current density inside the cable.
(ii) Integrate the displacement current density across the cross- section of the cable to find the total displacement current Id.
(iii) compare the conduction current I0 with the displacement current Id0.View SolutionWhat is the electric potential of the neutral wire in a main supply cable
View Solution
Knowledge Check
- Question 1 - Select One
A long straight cable contains 7 strands of wire each carrying a current of 5 A. The magnetic induction at a distance of 2 cm from the axis of the cable is
A5×10−5 TB3.5×10−4 TC3.5×10−4 TD1.1×10−3 T - Question 2 - Select One
A current i ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor of the cable, then the magnetic induction at any point outside the conductor at a distance r meter from the axis is
A∞BZeroCμ04π2irDμ04π2πrr - Question 3 - Select One
Current flows through a straight, thin-walled tube of radius r. The magnetic field at a distance x from the axis of the tube has magnitude B.
AB∝x, for 0 lt x lt rBB∝1/x , for 0 lt x lt rCB=0 , for 0≤x<rDB=0 , only for x=0
A wire carries an alternating current i=i0 sin omega t. In there an electric field in the vicinity of the wire?
View SolutionList the colours of the three wires in the cable connected to the plug of an electric iron.
View SolutionA coaxial cable consists of a thin inner current carrying conductor fixed along the axis of a hollow current conductor, Let B1 and B2 be the magnetic fields in the region between the conductors, and outside the conductor respectively.
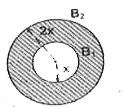 View Solution
View SolutionWhen there is an electric current through a conducting wire along its length, then an electric field must exist
View SolutionA solenoid of radius R number of turn per unit length n and length L has a current I=I0cosωt. The value of induced electric field at a distance of r outside the solenoid, is :
View Solution

