A long straight current carrying wire passes normally through the centre of circular loop. If the current through the wire increases, will there be an induced emf in the loop ? Justify.
To solve the problem, we need to analyze the situation using Faraday's law of electromagnetic induction. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the setup
We have a long straight current-carrying wire that passes normally (perpendicularly) through the center of a circular loop.
Hint: Visualize the arrangement to understand how the magnetic field from the wire interacts with the loop.
Step 2: Identify the magnetic field due to the wire
According to Ampere's law, a long straight current-carrying wire generates a magnetic field around it. The magnetic field (B) at a distance 'r' from the wire is given by the formula:
B=μ0I2πr
where I is the current through the wire and μ0 is the permeability of free space.
Hint: Remember that the magnetic field lines form concentric circles around the wire.
Step 3: Determine the magnetic flux through the loop
The magnetic flux (Φ) through the circular loop is given by:
Φ=B⋅A⋅cos(θ)
where A is the area of the loop and θ is the angle between the magnetic field lines and the normal to the surface of the loop.
Hint: In this case, since the wire passes normally through the center of the loop, the angle θ is 90 degrees.
Step 4: Calculate the magnetic flux
Since θ=90∘, we have:
cos(90∘)=0
Thus, the magnetic flux through the loop becomes:
Φ=B⋅A⋅0=0
Hint: Recognize that if the magnetic flux is zero, there is no change in flux to induce an EMF.
Step 5: Apply Faraday's law of electromagnetic induction
Faraday's law states that the induced EMF (E) in a closed loop is equal to the negative rate of change of magnetic flux through the loop:
E=−dΦdt
Since we found that the magnetic flux Φ is zero, any change in the current I through the wire does not change the flux linked with the loop.
Hint: Consider how the induced EMF relates to changes in magnetic flux.
Step 6: Conclusion
Since the magnetic flux linked with the loop is zero and does not change with an increase in current through the wire, the induced EMF in the loop is also zero. Therefore, there will be no induced EMF in the loop.
Final Statement: There will be no induced EMF in the loop as the magnetic flux linked with it remains zero, regardless of the increase in current through the wire.
We have a long straight current-carrying wire that passes normally (perpendicularly) through the center of a circular loop.
According to Ampere's law, a long straight current-carrying wire generates a magnetic field around it. The magnetic field (B) at a distance 'r' from the wire is given by the formula:
B=μ0I2πr
where I is the current through the wire and μ0 is the permeability of free space.
The magnetic flux (Φ) through the circular loop is given by:
Φ=B⋅A⋅cos(θ)
where A is the area of the loop and θ is the angle between the magnetic field lines and the normal to the surface of the loop.
Since θ=90∘, we have:
cos(90∘)=0
Thus, the magnetic flux through the loop becomes:
Φ=B⋅A⋅0=0
Faraday's law states that the induced EMF (E) in a closed loop is equal to the negative rate of change of magnetic flux through the loop:
E=−dΦdt
Since the magnetic flux linked with the loop is zero and does not change with an increase in current through the wire, the induced EMF in the loop is also zero. Therefore, there will be no induced EMF in the loop.
Topper's Solved these Questions
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SET-I (SECTION-B)
Explore 5 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SET-I (SECTION-C)
Explore 9 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SECTION-D
Explore 15 Videos
- SAMPLE PAPER 2019Book:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
A current- carrying straight wire is kept along the axis of a circular loop carrying a current. The straight wire
View SolutionA long wire carrying a steady current I lies in the plane of circular conducting loop placed at a certain distance from the wire. There will be an induced current in the loop if it is
View SolutionA very long uniformly charged rod falls with a constant velocity V through the centre of a circular loop. Then the magnitude of induced emf in the loop is
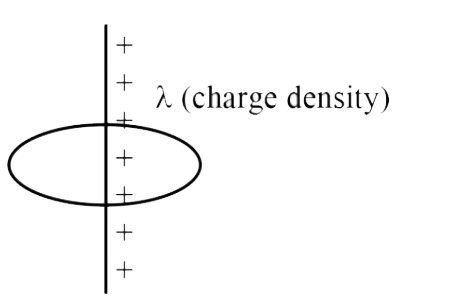
View SolutionA circular conducting loop of radius R carries a current I. Another straight infinite conductor carrying current I passes through the diameter of this loop as shown in the figure. The magnitude of force exerted by the straight conductor on the loop is
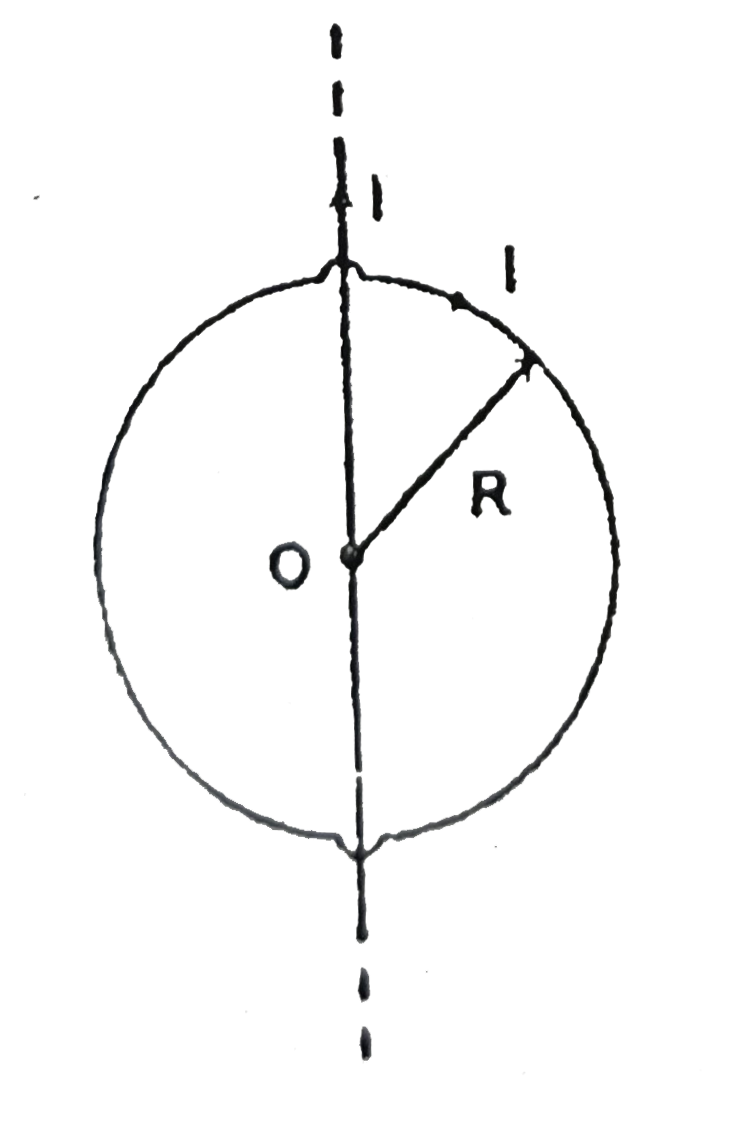
View SolutionA current carrying infinitely long wire is kept along the diameter of a circular wire loop, without touching it, the correct statements(s) is(are)
View SolutionA current carrying infinitely long wire is kept along the diameter of a circular wire loop, without touching it, the correct statements(s) is(are)
View SolutionA current carrying infinitely long wire is kept along the diameter of a circular wire loop, without touching it, the correct statements(s) is(are)
View SolutionA small, conducting circular loop is placed inside a long solenoid carrying a current. The plane of the loop contains the axis of the solenoid. If the current in the solenoid is varied, the current induced in the loop is
View SolutionA small, conducting circular loop is placed inside a long solenoid carrying a current. The plane of the loop contains the axis of the solenoid. If the current in the solenoid is varied, the current induced in the loop is
View SolutionIn Fig. there is a conducting loop ABCDEF of resistance λ per unit length placed near a long straight current-carrying wire. The dimension are shows in the figure. The long wire lies in the plane of the loop. The current in the long wire varies as I=I0(t).

The emf induced in the closed loop is
View Solution