A circular conducting loop of radius R carries a current I. Another straight infinite conductor carrying current I passes through the diameter of this loop as shown in the figure. The magnitude of force exerted by the straight conductor on the loop is
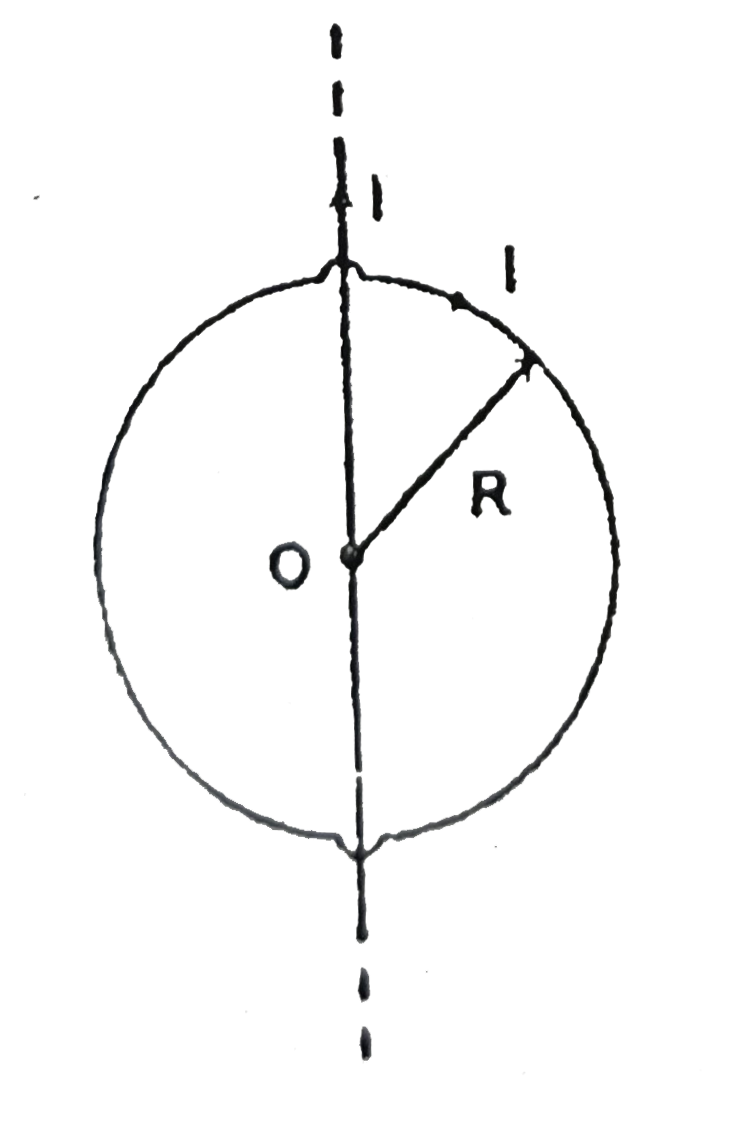
πμ0I2
μ0I2
μ0I22π
μ0I2π
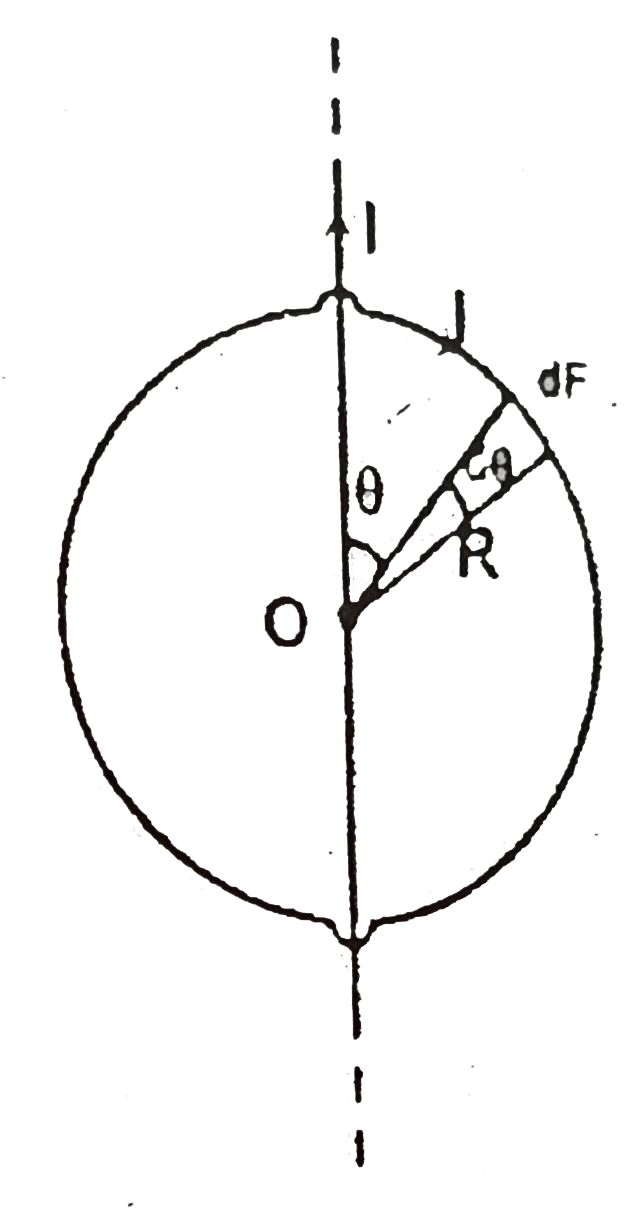
dF=(μ0I2πRsinθ).(Irdθ)
⇒Total forceF=∫dFsinθ
=∫2π0μ0I22πdθ=μ0I2
Similar Questions
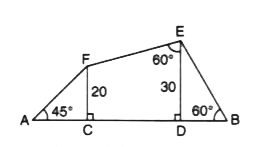
Find AB.
 View Solution
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionA circular loop of radius r carries a current i. where should a long , straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :
 View Solution
View SolutionIn given figure, current I is flowing through straight wire and divided equally in two loops as shown in the figure. The magnitude of magnetic field intensity at the center (O) is
View SolutionA circular loop of radius R carries a current I. Another circular loop of radius r(ltltR) carries a current I. The plane of the smaller loop makes an angle of 90^@ with that of the larger loop. The planes of the two circles are at right angle to each other. Find the torque acting on the smaller loop.
View SolutionA circular loop of radius r carries a current i. How should a long, straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the center becomes zero?
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
 View Solution
View SolutionA square loop ABCD , carrying a current I, is placed near and coplanar with a long straight conductor XY carrying a current I.
 View Solution
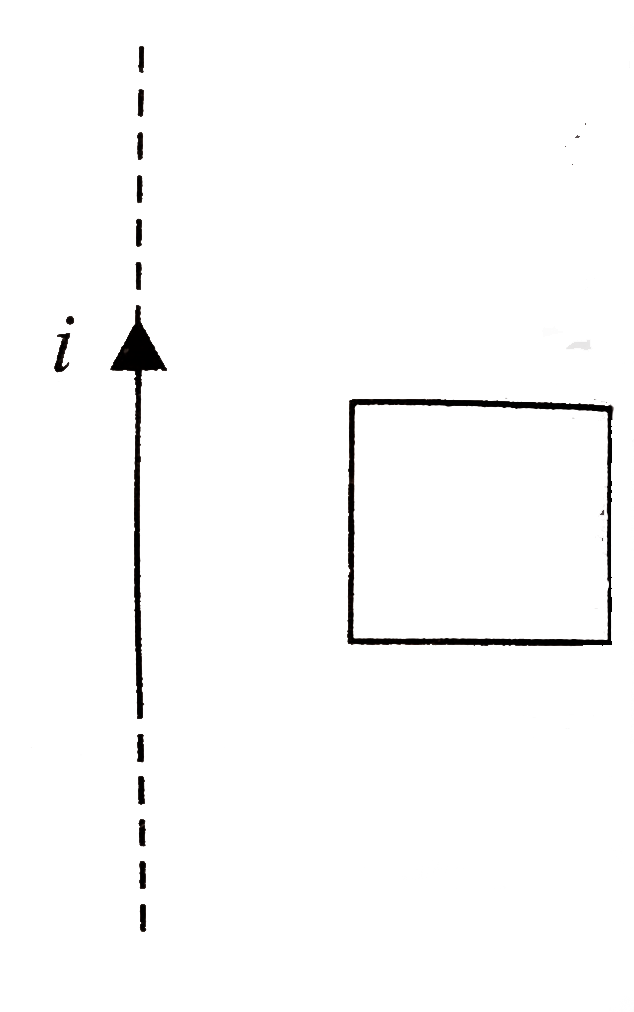
View SolutionA square conducting loop is placed in the neighbourhood of a coplaner long straight wire carrying a current i.
 View Solution
View Solution

