A long straight wire carrying current I and a square conducting wire loop of side l , at a distance 'a' from current wire as shown in the figure. Both the current wire and loop are in the plane of paper. Find the magnetic flux of current wire, passing through the loop.
μ02π.Illoge.a+Ia
μ04π.Illoge.a+Ia
μ02π.Il
μ04π.I
The correct Answer is:A
To find the magnetic flux of a long straight wire carrying current I passing through a square conducting wire loop of side l at a distance a from the current wire, we can follow these steps:
Step 1: Determine the Magnetic Field due to the Long Straight Wire
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
Step 2: Set Up the Geometry
The square loop is positioned such that its closest side is at a distance a from the wire. The distance from the wire to any point on the loop varies from a to a+l as we move from the closest side to the farthest side of the loop.
Step 3: Calculate the Magnetic Field at Different Points on the Loop
For a small strip of the loop at a distance x from the wire (where x ranges from a to a+l), the magnetic field B can be expressed as:
B(x)=μ0I2πx
Step 4: Calculate the Differential Area Element
The differential area dA for a small strip of width dx and height l is:
dA=ldx
Step 5: Calculate the Differential Magnetic Flux
The differential magnetic flux dΦ through the small strip is given by:
dΦ=B(x)⋅dA=(μ0I2πx)ldx
Step 6: Integrate to Find Total Magnetic Flux
To find the total magnetic flux Φ through the entire loop, we integrate dΦ from x=a to x=a+l:
Φ=∫a+laμ0Il2πxdx
Step 7: Perform the Integration
The integral of 1x is ln(x):
Φ=μ0Il2π(ln(x))a+la
Φ=μ0Il2π(ln(a+l)−ln(a))
Using the property of logarithms ln(m)−ln(n)=ln(mn):
Φ=μ0Il2πln(a+la)
Final Result
The magnetic flux Φ through the square loop is:
Φ=μ0Il2πln(a+la)
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
The square loop is positioned such that its closest side is at a distance a from the wire. The distance from the wire to any point on the loop varies from a to a+l as we move from the closest side to the farthest side of the loop.
For a small strip of the loop at a distance x from the wire (where x ranges from a to a+l), the magnetic field B can be expressed as:
B(x)=μ0I2πx
The differential area dA for a small strip of width dx and height l is:
dA=ldx
The differential magnetic flux dΦ through the small strip is given by:
dΦ=B(x)⋅dA=(μ0I2πx)ldx
To find the total magnetic flux Φ through the entire loop, we integrate dΦ from x=a to x=a+l:
Φ=∫a+laμ0Il2πxdx
The integral of 1x is ln(x):
Φ=μ0Il2π(ln(x))a+la
Φ=μ0Il2π(ln(a+l)−ln(a))
Using the property of logarithms ln(m)−ln(n)=ln(mn):
Φ=μ0Il2πln(a+la)
The magnetic flux Φ through the square loop is:
Φ=μ0Il2πln(a+la)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Example Type 1
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Example Type 2
Explore 2 Videos
- CURRENT ELECTRICITYBook:DC PANDEYChapter:CURRENT ELECTRICITYExercise:Medical entrances gallery
Explore 97 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEYChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
Similar Questions
A square loop is placed near a long current carrying straight wire as shown in the figure . Match the following table


View SolutionA rectangular loop is placed near a current carrying straight wire as shown in the figure. If the loop is rotated about an axis passing throught one of its sides find the direction of induced current in the loop.
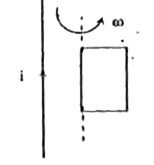
View Solution
Knowledge Check
A long straight wire is carrying a current of 25 A. A square loop of side length 10 cm carrying a current of 15 A, is placed 2 cm from the wire as shown in figure. The force on the loop is
 A3.1×10−3N towards the wireB3.1×10−4N towards from the wireC9.4×10−4N towards the wireD9.4×10−4N away from the wire.
A3.1×10−3N towards the wireB3.1×10−4N towards from the wireC9.4×10−4N towards the wireD9.4×10−4N away from the wire.A long wire carrying a steady current I lies in the plane of circular conducting loop placed at a certain distance from the wire. There will be an induced current in the loop if it is
Amoved parallel to the wireBroatated about an axis perpendicular to the plane of the loop passing through the centre of the loopCrotated about an axis parallel to the wire passing through the centre of the loopDmoved away from the wireA current carrying squre loop is placed near an infinitely long current carrying wire as shown in figure . The loop torque acting on the loop is
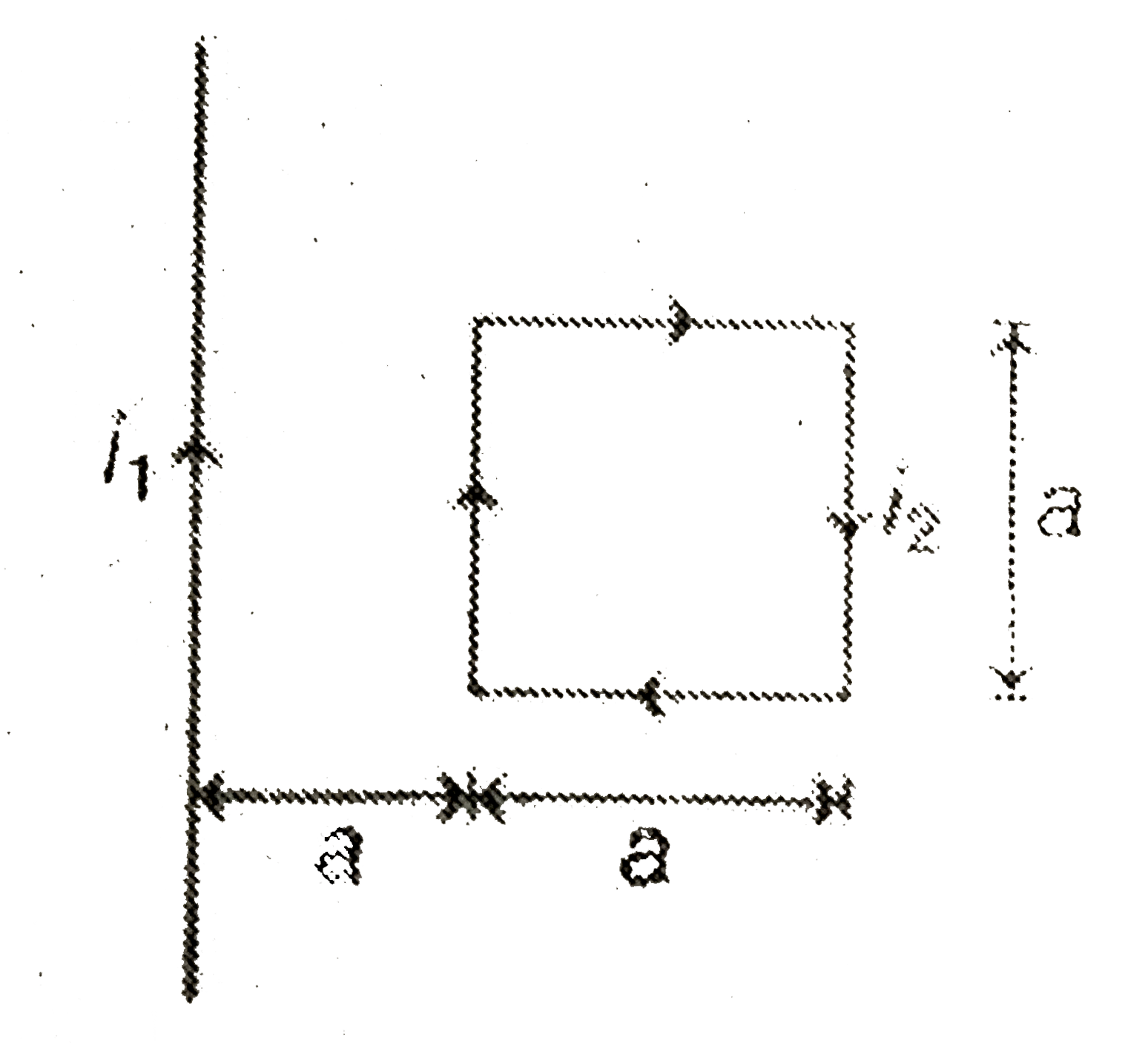 Aμ02πi1i2rBμ02πi1i2loge2Cμ02πi1i2r2DZero
Aμ02πi1i2rBμ02πi1i2loge2Cμ02πi1i2r2DZero
A circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop

View SolutionA square shaped current carrying loop MNOP is placed near a straight long current carrying wire AB as shown in the figure. The wire and the loop lie in the same plane. If the loop experiences a net force F towards the wire, find the magnitude of the force on the side 'NO" of the loop.
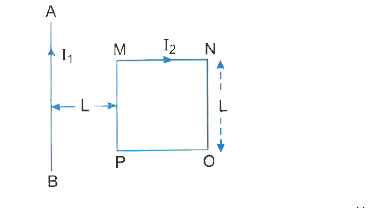
View SolutionA straight wire carrying a current is turned into a circular loop if the magnitude of magnetic moment associated with it is M then the length of the wire will be
View SolutionA current carrying squre loop is placed near an infinitely long current carrying wire as shown in figure . The loop torque acting on the loop is

View SolutionA long straight wire is carrying current I in + z direction .The x-y plane contains a closed circular loop carrying current I2 and not encircling the straight wire.The force on the loop will be
View Solution