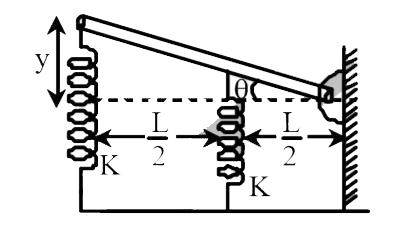
A long uniform rod of length $L$ and mass $M$ is free to rotate in a horizontal plane about a vertical axis through its one end 'O'. A spring of force constant $k$ is connected between one end of the rod and $P Q$ . When the rod is in equilibrium it is parallel to $P Q$ .

(a)What is the period of small oscillation that result when the rod is rotated slightly and released ?
(b) What will be the maximum speed of the displacement end of the rod, if the amplitude of motion is $θ_{0}$ ?

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

(a) Restoring torque about 'O' due to elastic of the spring
$τ = - F L = - k y L (F = k y)$
$τ = - k L^{2} θ$ (as $y = L θ$ )
$τ = I α = \frac{1}{3} M L^{2} \frac{d^{2} θ}{{d t}^{2}}$
$\frac{1}{3} M L^{2} \frac{d^{2} θ}{{d t}^{2}} = - k L (2) θ$
$\frac{d^{2}}{{d t}^{2}} = - \frac{3 k}{M} θ$
$ω = \sqrt{\frac{3 k}{M}}$
$\Rightarrow T = 2 π \sqrt{\frac{M}{3 k}}$
(b) In angular SHM, maximum angular velocity
${(\frac{d θ}{d t})}_{max} = θ_{0} ω = \sqrt{\frac{3 k}{M}}$
$v = r (\frac{d θ}{d t})$
So , $v_{max} = L {(\frac{d θ}{d t})}_{max} = L θ_{0} \sqrt{\frac{3 k}{M}}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all points
Bdifferent at differen points and maximum at centre of rod
Cdifferent at different points and minimum at axis of rotation.
Ddifferent at different points and maximum at axis of rotation
Question 2 - Select One
A uniform rod of mass $m$ and length $l$ rotates in a horizontal plane with an angular velocity $ω$ about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A $\frac{1}{2} m ω^{2} x$
B $\frac{1}{2} m ω^{2} (1 - \frac{x^{2}}{l})$
C $\frac{1}{2} m ω^{2} l (1 - \frac{x^{2}}{l^{2}})$
D $\frac{1}{2} m ω^{2} l [1 - \frac{x}{l}]$
Question 3 - Select One
A thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity $ω$ in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
A $\frac{m ω^{2} l^{2}}{6 A Y}$
B $\frac{m ω^{2} l^{2}}{3 A Y}$
C $\frac{m ω^{2} l^{2}}{A Y}$
D $\frac{m ω^{2} l^{2}}{2 A Y}$

DC PANDEY-SIMPLE HARMONIC MOTION-Miscellaneous Examples

Home
Ask Doubt
Profile