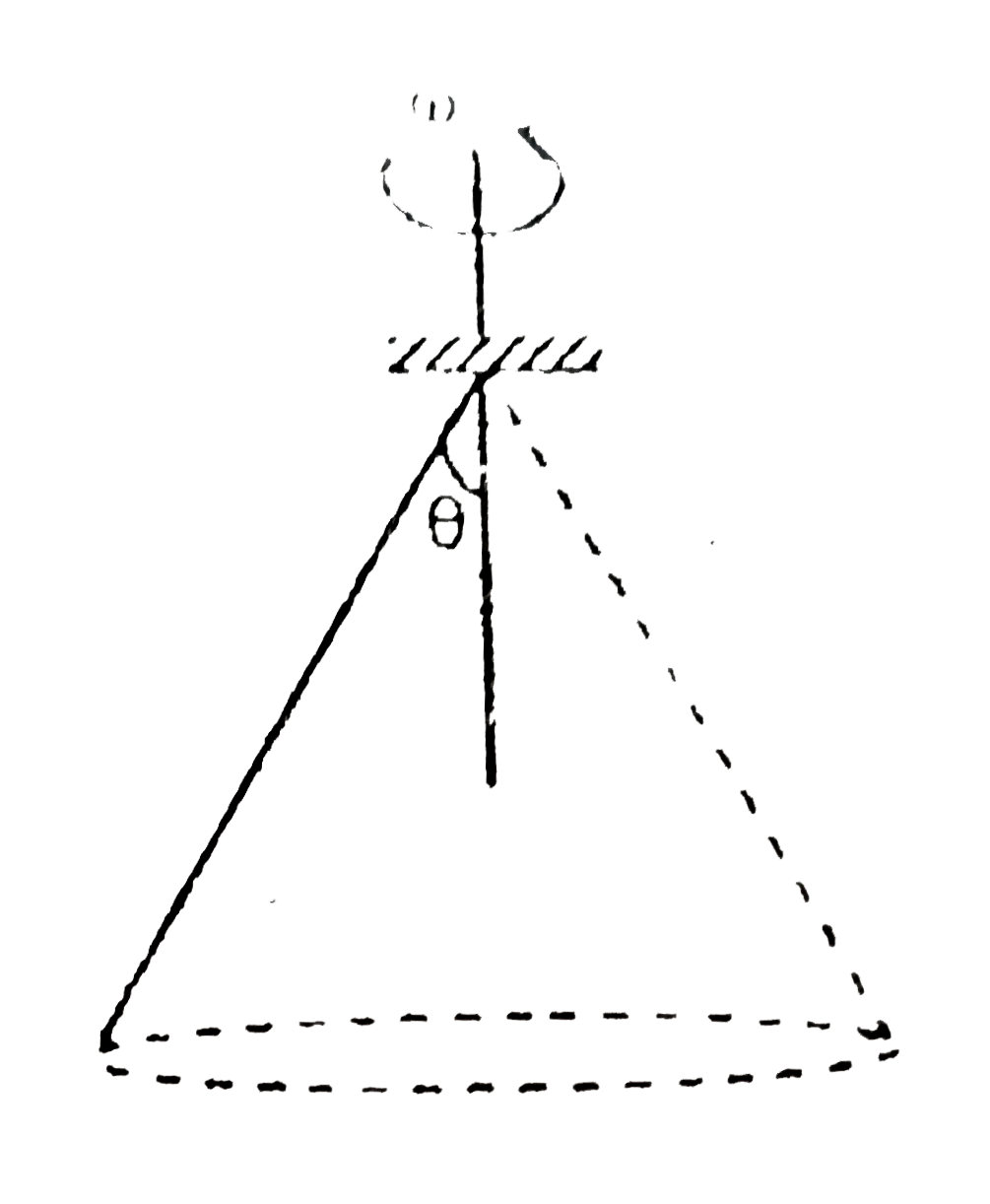
A conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity ω(the upper end of the rod is hinged). Find the angle θ between the rod and the vertical.
Let us consider the system in a frame rotating with the rod. In this frame, the rod is at rest and experiences not only the gravitational force m→g and the reaction force →R, but also the centrifugal force →Fcf.
In the considered frame, from the condition of equilibrium i.e. N0z=0
or, Ncf=mg12sinθ (1)
where Ncf is the moment of centrifugal force about O. To calculate Ncf, let us consider an element of length dx, situated at a distance x from the point O. This element is subjected to a horizontal pseudo force (ml)dxω2xsinθ.
The moment of this pseudo force about the axis of rotation through the point O is
dNcf=(ml)dxω2xsinθxcosθ
=mω2lsinθcosθx2dx
So Ncf=l∫0mω2lsinθcosθx2dx=mω2l23sinθcosθ (2)
It follows from Eqs. (1) and (2) that,
cosθ=(3g2ω2l) or θ=cos−1(3g2ω2l) (3)

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Elastic Deformation Of Asolid Body
Explore 25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Hydrodynamics
Explore 25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A conical pendulum consisting of rigid rod of length l and mass m rotates uniformly about vertical axis with angular velocity ω. Find the angle θ between the rod and the vertical
[Hint : Equate the moments of centrifugal forces on elementary masses to the moment of gravity]
View SolutionA uniform rod AB of length 2l and mass m is rotating in a horizontal plane about a vertical axis through A, with angular velocity ω, when the mid-point of the rod strikes a fixed nail and is brought immediately to rest. Find the impulse exerted by the nail.
View Solution
Knowledge Check
A rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
 Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)A uniform rod of length l is from rest such that it rotates about a smooth pivot. The angular speed of the rod when it becomes vertical is.
 .A2√6g7lB√6g7lC2√3g7lD√3g7l
.A2√6g7lB√6g7lC2√3g7lD√3g7l
A thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA uniform of mass m and length L is tied to a vertical shaft. It rotates in horizontal plane about the vertical axis at angular velocity ω. How much horizontal force does the shaft exert on the rod?

View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA copper rod of length L rotates with an angular with an angular speed 'ω' in a uniform magnetic field B. find the emf developed between the two ends of the rod. The field in perpendicular to the motion of the rod.
View Solution