A machinist starts with three identical square plates but cuts one corner from one of them, two corners from the second and three corners from the third. Rank the three according to the x-coordinate of their centre of mass, from smallest to largest.
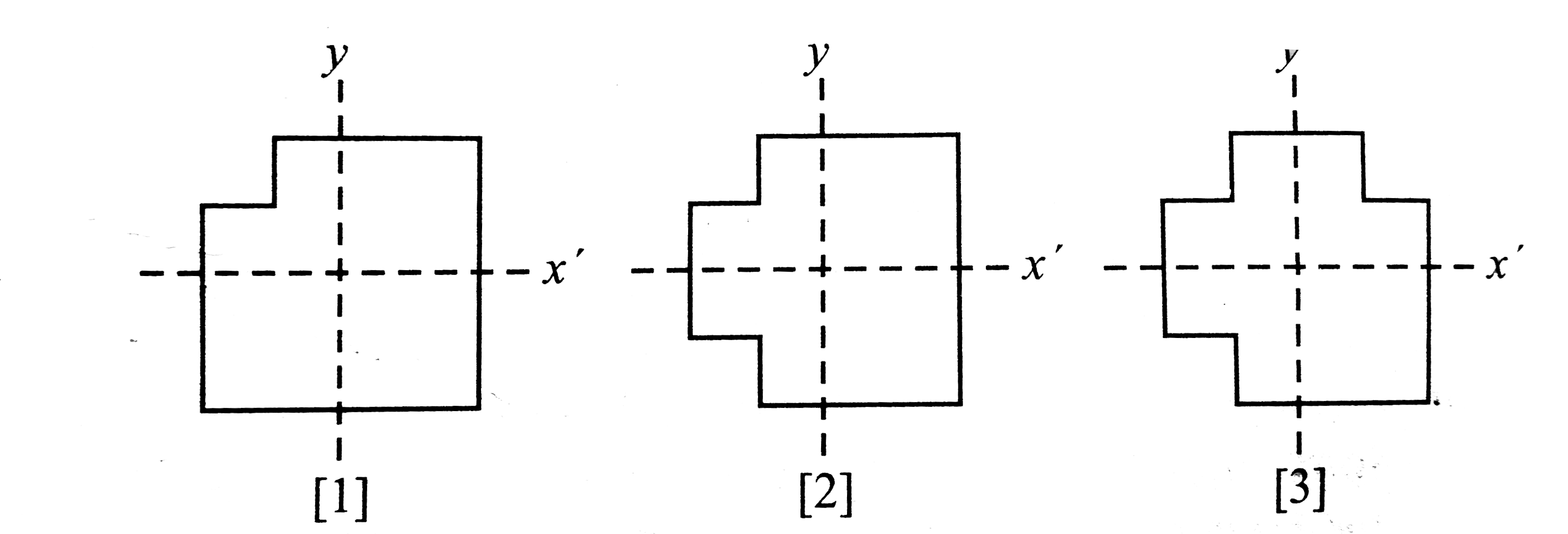
3,1,2
1,3,2
3,2,1
1 and 3 tie, then 2
The correct Answer is:B

x1=(mxM−m)∣∣∣x2=(2mxM−2m)∣∣∣x3=(mxM−3m)
x1<x3<x2
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
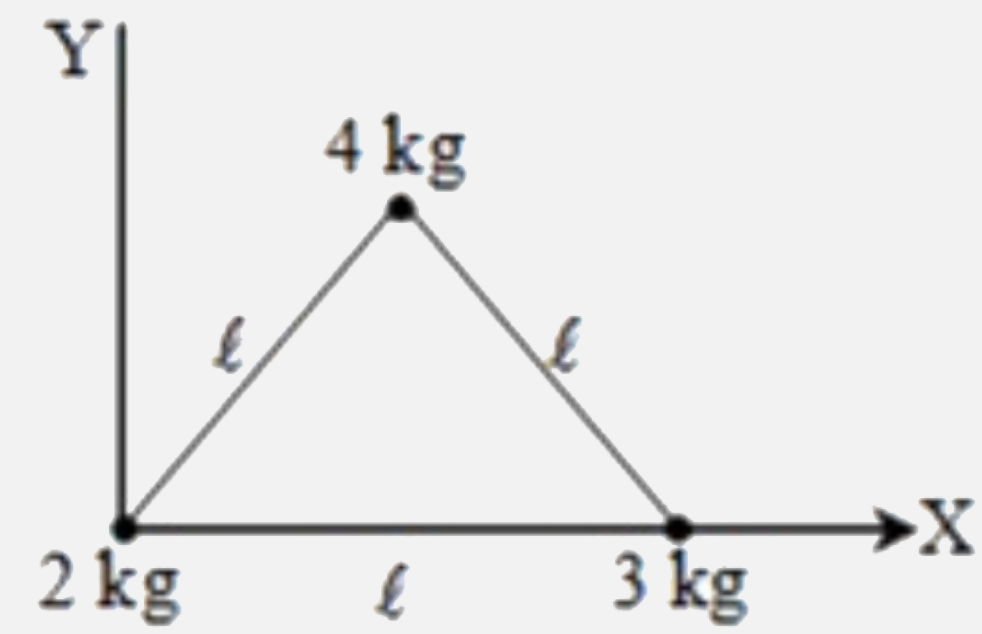
Three masses 2 kg , 3kg and 4kg are lying at the corners of an equilateral triangle of side I. The X coordinate of center of mass is
View SolutionThree particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
View Solution
Knowledge Check
A uniform wire is bent into the form of a rectangle of length L and width W. The coordinates of its centre of mass from a corner are
A(0,0)B(L2,W)C(L,W2)D(L2,W2)Three identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
A√3(I∩−j∩)BI∩√3+j∩CI∩+j∩3DI∩+j∩√3Three identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
A√3(I∩−j∩)BI∩√3+j∩CI∩+j∩3DI∩+j∩√3
Three identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
View SolutionA square of side a charge Q at its centre and charge q at one of the corners. The work required to be done in moving the charge q from the corner to the diagonally opposite corner is
View SolutionA square of side a has charge Q at its centre and charge q at one of the corners. The work required to be done in moving the charge q from the corner to the digitally opposite corner is :
View SolutionA square of side a has charge Q at its centre and charge q at one of the corners. The work required to be done in moving the charge q from the corner to the digitally opposite corner is :
View SolutionThree identical particles each of mass 0.1kg are arranged at three corners of a square of side √2m. The distance of the centre of mass from the fourth corners is
View Solution
