Three particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
The correct Answer is:A
To find the distance of the center of mass from point A for three particles of masses 1 kg, 2 kg, and 3 kg placed at the corners of an equilateral triangle ABC with an edge length of 1 m, we can follow these steps:
Step 1: Define the coordinates of the particles
- Let the coordinates of the particles be:
- A (1 kg) at (0, 0)
- B (2 kg) at (1, 0)
- C (3 kg) at (12,√32)
Step 2: Calculate the total mass
- The total mass M of the system is:
M=mA+mB+mC=1kg+2kg+3kg=6kg
Step 3: Calculate the center of mass coordinates
- The center of mass Rcm can be calculated using the formula:
Rcm=1M∑miri
where mi is the mass and ri is the position vector of each particle.
- Calculate the x-coordinate of the center of mass:
xcm=1M(mA⋅xA+mB⋅xB+mC⋅xC)
xcm=16(1⋅0+2⋅1+3⋅12)=16(0+2+32)=16⋅72=712
- Calculate the y-coordinate of the center of mass:
ycm=1M(mA⋅yA+mB⋅yB+mC⋅yC)
ycm=16(1⋅0+2⋅0+3⋅√32)=16(0+0+3√32)=3√312=√34
Step 4: Write the position of the center of mass
- The center of mass Rcm is located at:
Rcm=(712,√34)
Step 5: Calculate the distance from point A
- The distance d from point A to the center of mass can be calculated using the distance formula:
d=√(xcm−xA)2+(ycm−yA)2
d=
⎷(712−0)2+(√34−0)2
d=
⎷(712)2+(√34)2
d=√49144+316
- Convert 316 to a fraction with a denominator of 144:
316=27144
d=√49+27144=√76144=√7612=2√1912=√196
Final Answer
The distance of the center of mass from point A is:
√196meters
---
- Let the coordinates of the particles be:
- A (1 kg) at (0, 0)
- B (2 kg) at (1, 0)
- C (3 kg) at (12,√32)
- The total mass M of the system is:
M=mA+mB+mC=1kg+2kg+3kg=6kg
- The center of mass Rcm can be calculated using the formula:
Rcm=1M∑miri
where mi is the mass and ri is the position vector of each particle.
xcm=1M(mA⋅xA+mB⋅xB+mC⋅xC)
xcm=16(1⋅0+2⋅1+3⋅12)=16(0+2+32)=16⋅72=712
ycm=1M(mA⋅yA+mB⋅yB+mC⋅yC)
ycm=16(1⋅0+2⋅0+3⋅√32)=16(0+0+3√32)=3√312=√34
- The center of mass Rcm is located at:
Rcm=(712,√34)
- The distance d from point A to the center of mass can be calculated using the distance formula:
d=√(xcm−xA)2+(ycm−yA)2
d=
⎷(712−0)2+(√34−0)2
d=
⎷(712)2+(√34)2
d=√49144+316
- Convert 316 to a fraction with a denominator of 144:
316=27144
d=√49+27144=√76144=√7612=2√1912=√196
The distance of the center of mass from point A is:
√196meters
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.26videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.37videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - MiscellaneousExamples9videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
Similar Questions
Three particles of msses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre ofmass of the system.
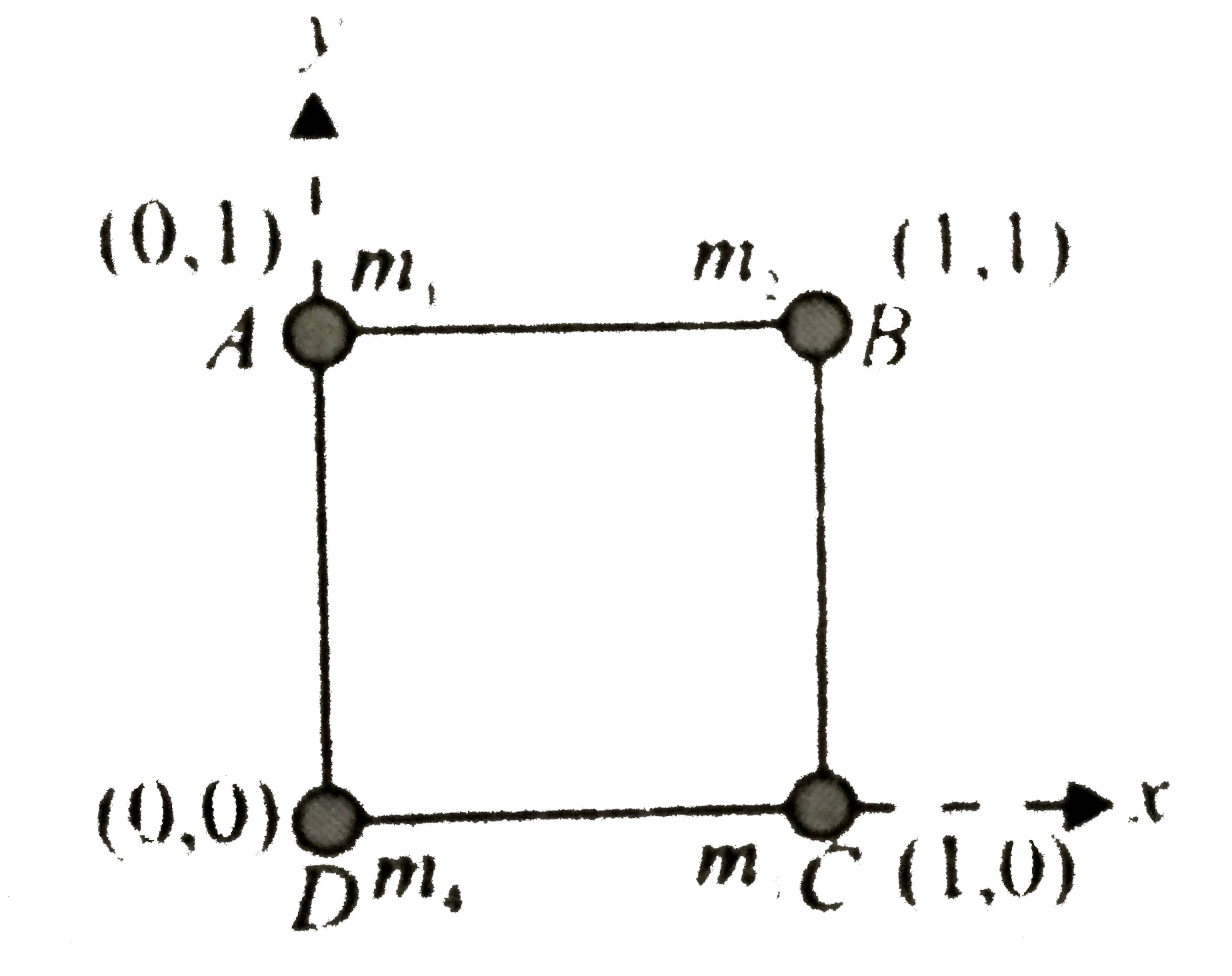
View SolutionFour particles of masses 1kg,2kg,3kg and 4kg are placed the four vertices A,B,C and D, respectively, of a square of side 1m. Find the position of centre of mass of the particles.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Three particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
A√6mB√2mC1√2mD2m - Question 2 - Select One
Four particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
A(0.5,0.3)B(0.4,0.3)C(0.5,0.8)D(0.7,0.3)
3Masses 8 kg, 2 kg, 4 kg and 2 kg are placed at the corners A, B, C, D respectively of a square ABCD of diagonal 80 cm. The distance of centre of mass from A will be
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A,B,C and D of a square of side 1m. Find square of distance of their centre of mass from A.
View SolutionThree sperical balls of masses 1kg,2kg and 3kg are placed at the corners of an equilateral triangle of side 1m. Find the magnitude of the gravitational force exerted by 2kg and 3kg masses on 1kg mass.
View SolutionThree point masses m1=2Kg,m2=4kgandm3=6kg are kept at the three corners of an equilateral triangle of side 1 m. Find the locationo of their center of mass.
View SolutionThree spherical balls of masses 1 kg, 2 kg and 3 kg are placed at the corners of an equilaterial triangle of side 1m.Find the magnitude of the gravitational force exerted by 2 kg and 3 kg masses on 1 kg mass.
View SolutionThree particles of msses 1.0 kg , , 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
View Solution

