A magnetic field induction is changing in magnitude at a constant rate . A given mass of copper is drawn into a wire of radius and formed into a loop of radius is placed perpendicular to the field. Show that induced current in the loop is given by
: resistivity, : density of copper.
Step by step video, text & image solution for A magnetic field induction is changing in magnitude at a constant rate dB//dt . A given mass m of copper is drawn into a wire of radius alpha and formed into a loop of radius r is placed perpendicular to the field. Show that induced current in the loop is given by i=(m)/(4pipdelta)(dB)/(dt) p : resistivity, delta : density of copper. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Practice Exercise 5.3
13 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Practice Exercise 5.4
13 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Practice Exercise 5.1
12 Videos
- CURRENT ELECTRICITYBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
389 Videos
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Unsolved Numberical Problems
73 Videos
Similar Questions
A magnetic field induction is changing in magnitude at a constant rate dB/dt . A given mass m of copper is drawn into a wire into a wire of radius α and formed into a loop of radius r is placed perpendicular to the field. Show that induced current in the loop is given by im4πpδdBdt
p : resistivity, δ : density of copper.
View SolutionA current carrying loop of radius R and mass 'm' is placed inside a uniform magnetic field an shown

View Solution
Knowledge Check
A magnetic field induction is changing in magnitude in a region at a constant rate dB/dt. A given mass m of copper drawn into a wire and formed into a loop is placed perpendicular to the field. If the values of specific resistance and density of copper are ρ and σ respectively, then the current in the loop is given by :
A4πmρσdBdtBm4πρσdBdtCmρσdBdtD2πmρσdBdtThe magnetic field perpendicular to the plane of a conducting ring of radius r change ate the rate dBdt
AThe emf induced in the ring is πr2dBdtBThe emf induced in the rintg is 2πrdBdtCThe potential difference between diametrically opposite points on the ring is half of the induced emf.DAll points on the ring are at the same potential.A circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
Aremain unchangedBis doubledCis halvedDbecomes 4 times
A unifrom magnetic field B points vertically up and is slowly changed in magnitude, but not in direction. the rate of change of the magnetic field is α .A conducting ring of radius r and resistance R is held perpendicular to the megnetic field, and is totally inside it. The induced current in the ring is
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
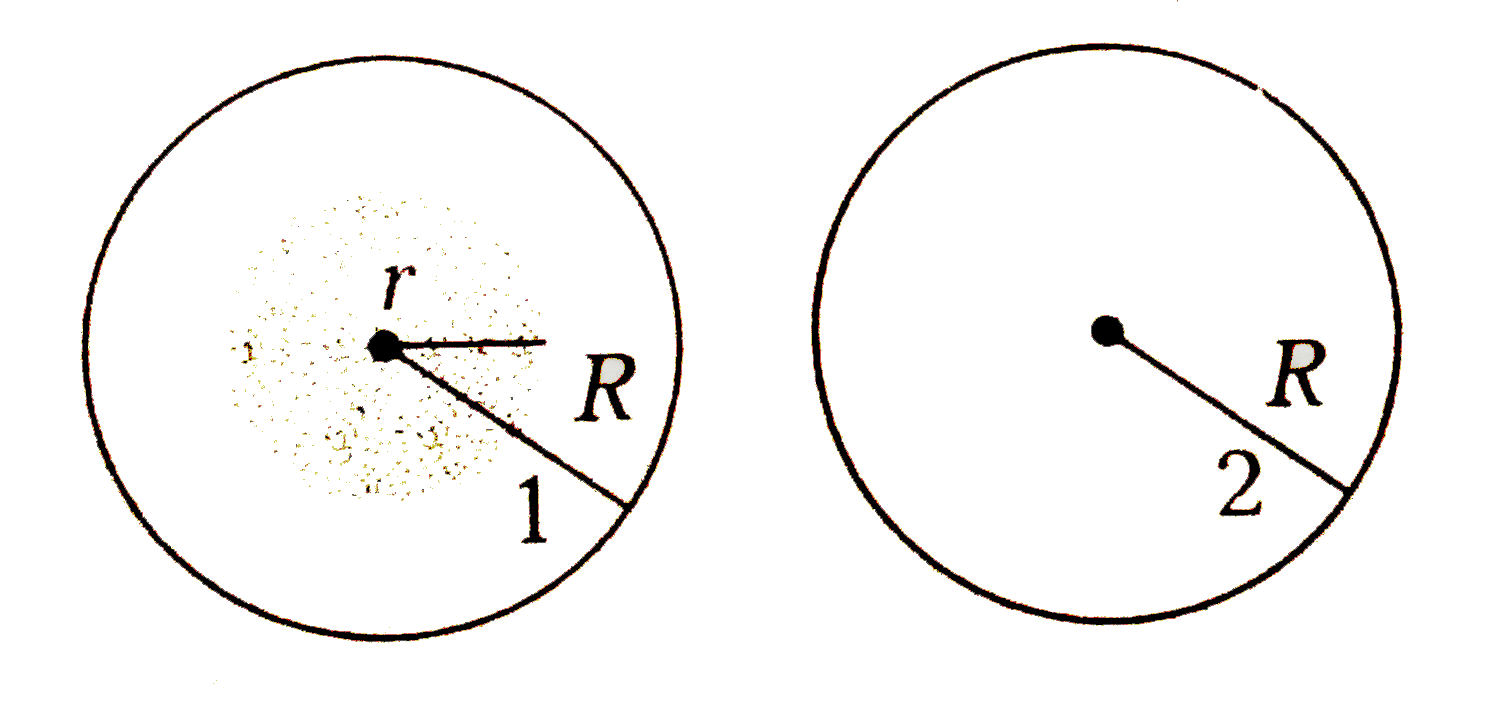
View SolutionA uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate dBdt. Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
View SolutionA conducting circular loop of radius r carries a constant current i.It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is
View SolutionA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is
View Solution
