A magnetic field →B=−B0ˆi exists within a sphere of radius R=v0T√3 where T is the time period of one revolution of a charged particle starting its motion from origin and moving with a velocity →v0=v02√3ˆi−v02ˆj. Find the number of turns that the particle will take to come out of the magnetic field.
5
1
4
2
The correct Answer is:D
v⊥er=−v02 will contribute to circular motion.
v∣∣=v0√32 will contribute to helical path.
T=2πmB0q
Pitch, P=v∣∣T=v0√32T
Numbers of turns =RP=v0T√3(2)v0√3T=2
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Section B - Assertion Reasoning
31 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - AIPMTNEET Questions
47 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Circular Arc
69 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
A magnetic field →B=−B0ˆi exists within a sphere of radius R=v0T√3 where T is the time period of one revolution of a charged particle starting its motion form origin and moving with a velocity vce(v)0=v02√3ˆi−v02ˆj. Find the number of turns that the particle will take to come out of the magnetic field.
View SolutionWhat is the direction of the force acting on a charged particle q, moving with a velocity →v a uniform magnetic field →B ?
View Solution
Knowledge Check
A charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
Maximum z-coordinate of the particle isA√3mv0B0qB2√3mv0B0qC2mv0B0qDmv0B0qA magnetic field →B=B0ˆj , exists in the region a<x<2a , and vec(B) = -B_(0) hat(j),∈theregion2a lt xlt 3a,whereB_(0)isapositiveconstant.Apositivep∮char≥mov∈gwithavelocityvec(v) = v_(0) hat (i),wherev_(0) is a positive constant , enters the magnetic field at x=a . The trajectory of the charge in this region can be like
 A
A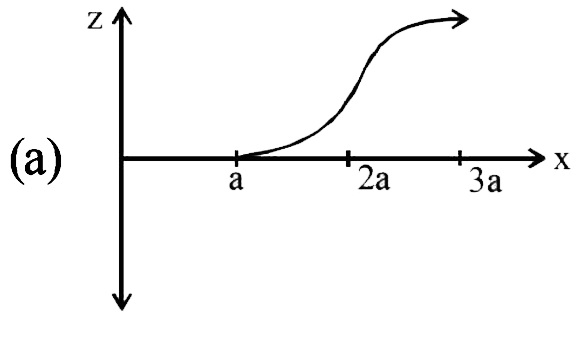 B
B C
C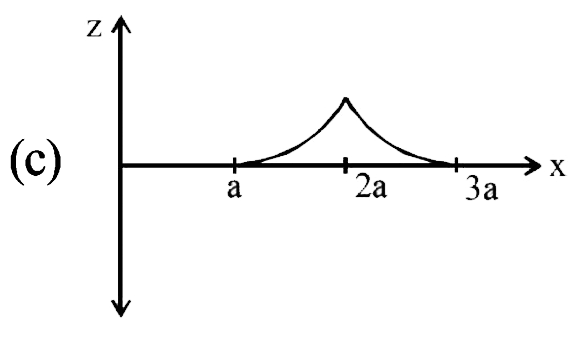 D
D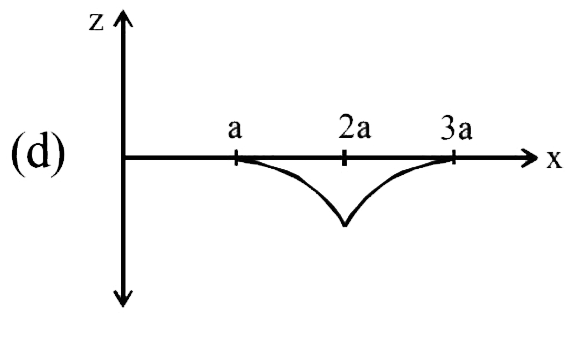
A charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
Pitch of the helical path described by the particle isA2πmv0B0qB√3πmv02B0qCπmv0B0qD2√3πmv0B0q
A particle of specific charge 'α' is projected from origin at t=0 with a velocity →V=V0(ˆi−ˆk) in a magnetic field →B=−B0ˆk. Then : (Mass of particle =1 unit)
View SolutionA portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton
View SolutionUnder the influence of a uniform magnetic field, a charged particle moves with constant speed v in a circle of radius r. The time period of revolution of the particle
View SolutionA charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
When z-co-ordinate has its maximum value
View SolutionAssertion: A charged particle enters in a magnetic field B=B0ˆiwithvelocityv=v0ˆi+v0ˆj, then minimum speed of charged particle may be v0.
Reason: A variable acceleration particle may be v0.
View Solution
