A man can swim with velocity v relative to water. He has to cross a river of width d flowing with a velocity u(u>v). The distance traveled by man along the flow is x, when he reaches to opposite bank. For x to be minimum the person should swim at an angle α with the direction of the flow of water, where α is
sin−1(v/u)
sin−1(u/v)
π2+sin−1(v/u)
π2+sin−1(u/v)
The correct Answer is:C
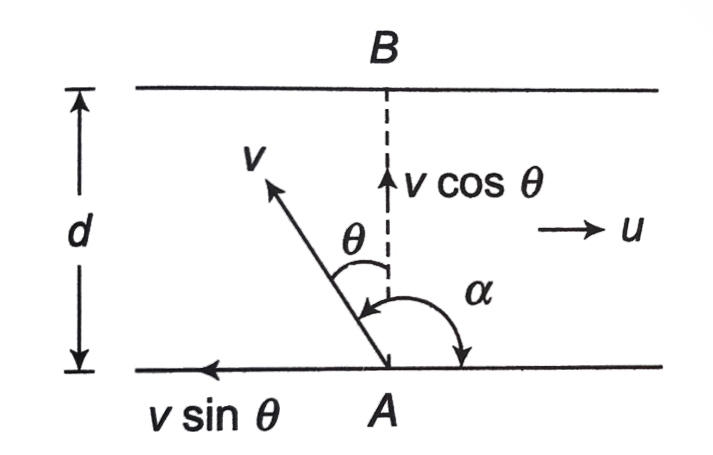
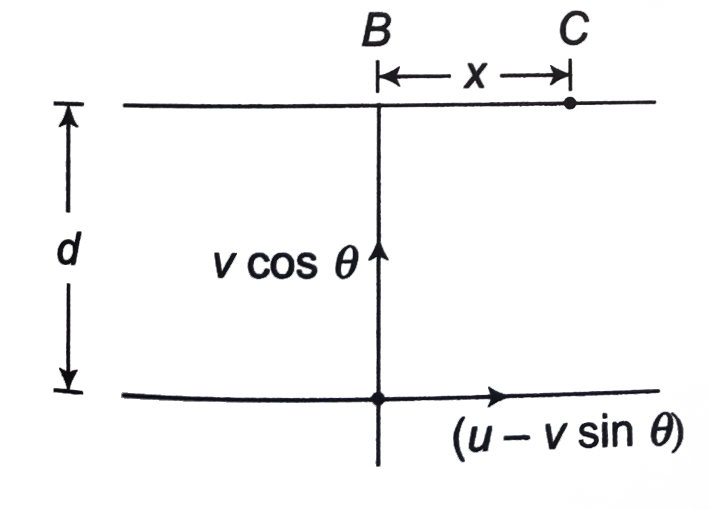
y:d=vcosθt⇒t=dvcosθ
x:x=(u−vsinθ)t=(u−vsinθ)dvcosθ
=(uvsecθ−tanθ)d
For x to be minimum
dxdθ=d(uvsecθtanθ−sec2θ)=0
uvtanθ=secθ
sinθ=vu
α=90∘+θ=π2+sin−1(vu)
Topper's Solved these Questions
Similar Questions
A man can swim with velocity v relative to water. He has to cross a river of width d flowing with a velocity u(u>v). The distance through which he is carried down stream by the river is x. Which of the following statements is correct?
View SolutionA swimmer capable of swimming with velocity v relative to water jumps in a flowing friver having velocity u. The man swims a distance d down stream and returns back to the priginal position. Find out the time taken in complete motion.
View Solution
Knowledge Check
- Question 1 - Select One or More
A man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
AThe minimum time in which he can cross the river is bvBHe can reach a point exactly opposite on the bank in time t=b√v2−u2ifv>uCHe cannot reach a point exactly opposite on the bank if u>vDHe cannot reach a point exactly opposite on the bank if v>u - Question 2 - Select One or More
A man who can swim at a speed v relative to the water wants to cross a river of width d flowing with a speed u. The point opposite him across the river is A.
AHe can reach the point A in time d/vBHe can reach the point A is time d√v2−u2CThe minimum time in which he can cross river is dvDHe can not reach A if u gt v - Question 3 - Select One or More
A man who can swim at a speed v relative to the water wants to cross a river of width d, flowing with a speed u. The point opposite him across the river is P.
AThe minimum time in which he can cross the river is dvBHe can reach the point P in time dvCHe can reach the point P in time d√v2−u2DHe cannot reach P if u>v
A man can swim with a speed v relative to water . There is a river of width d which is flowing at a speed u . A is the point on river bank from where he starts and B is point directly opposite to A on the other side of the river .
View SolutionA boat crossing a river moves with a velocity v relative to still water. The river is flowing with a velocity v/2 with respect to the bank. The angle with respect to the flow direction with which the boat should move to minimize the drift is–
View SolutionPerson aiming to reach the exactly opposite point on the bank of a stream is swimming with a speed of 0.5ms−1 at an angle of 120∘ with the direction of flow of water.The speed of water in the stream is
View SolutionA person aiming to reach the exactly opposite point on the bank of a stream is swimming with a speed of 0.5ms at an angle of 120∘ with the direction of flow of water. The speed of water in the stream is
View SolutionA person aiming to reach exactly opposite point on the bank of a stream is swimming with a speed of 0.6 m/s at an angle of 120∘ with the direction of flow of water . The speed of water in the stream is
View Solution

