A man directly crosses a river in time and swims down the current a distance equal to the width of the river I time . If be the speed of the current and the man respectively, show that : : : : .
Step by step video & image solution for A man directly crosses a river in time t_1 and swims down the current a distance equal to the width of the river I time t_2. If u and v be the speed of the current and the man respectively, show that t_1: t_2: : sqrt(v + u) : sqrt(v - u)). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTORSBOOK - SL ARORACHAPTER - VECTORSEXERCISE - Problems For Self Practice
56 Videos
- VECTORSBOOK - SL ARORACHAPTER - VECTORSEXERCISE - TYPE F
2 Videos
- Units and MeasurementsBOOK - SL ARORACHAPTER - Units and MeasurementsEXERCISE - Exercise
499 Videos
- WAVE MOTIONBOOK - SL ARORACHAPTER - WAVE MOTIONEXERCISE - All Questions
271 Videos
Similar Questions
Knowledge Check
A man wishes to cross a river flowing with velocity u swims at an angle θ with the river flow.If the man swims with speed vand if the width of the river is d, then the drift travelled by him is
A(u+vcosθ)dvsinθB(u−vcosθ)dvsinθC(u−vcosθ)dvcosθD(u+vcosθ)dvcosθA man crosses the river perpendicular to river in time t seconds and travels an equal distance down the stream in T seconds. The ratio of man's speed in still water to the river water will be:
At2−T2t2+T2BT2−t2T2+t2Ct2+T2t2−T2DT2+t2T2−t2A man swims to and fro along the bank of a river with a velocity v relative to water. If the velocity of flow is u, the average speed of the man (for to and fro motion) is :
A0B√uvCu+v2Dv2−u2v
A man wants to swim in a river from A→B and back from B→A always following line AB (Fig. 5.94). The distance between points AandB is S. The velocity of the river current v is constant over the entire width of the river. The line AB makes an angle ∝ with the direction of current. The man moves with velocity u at angle β to the line AB. The man swim to cover distance AB and back, find the time taken to complete the journey.
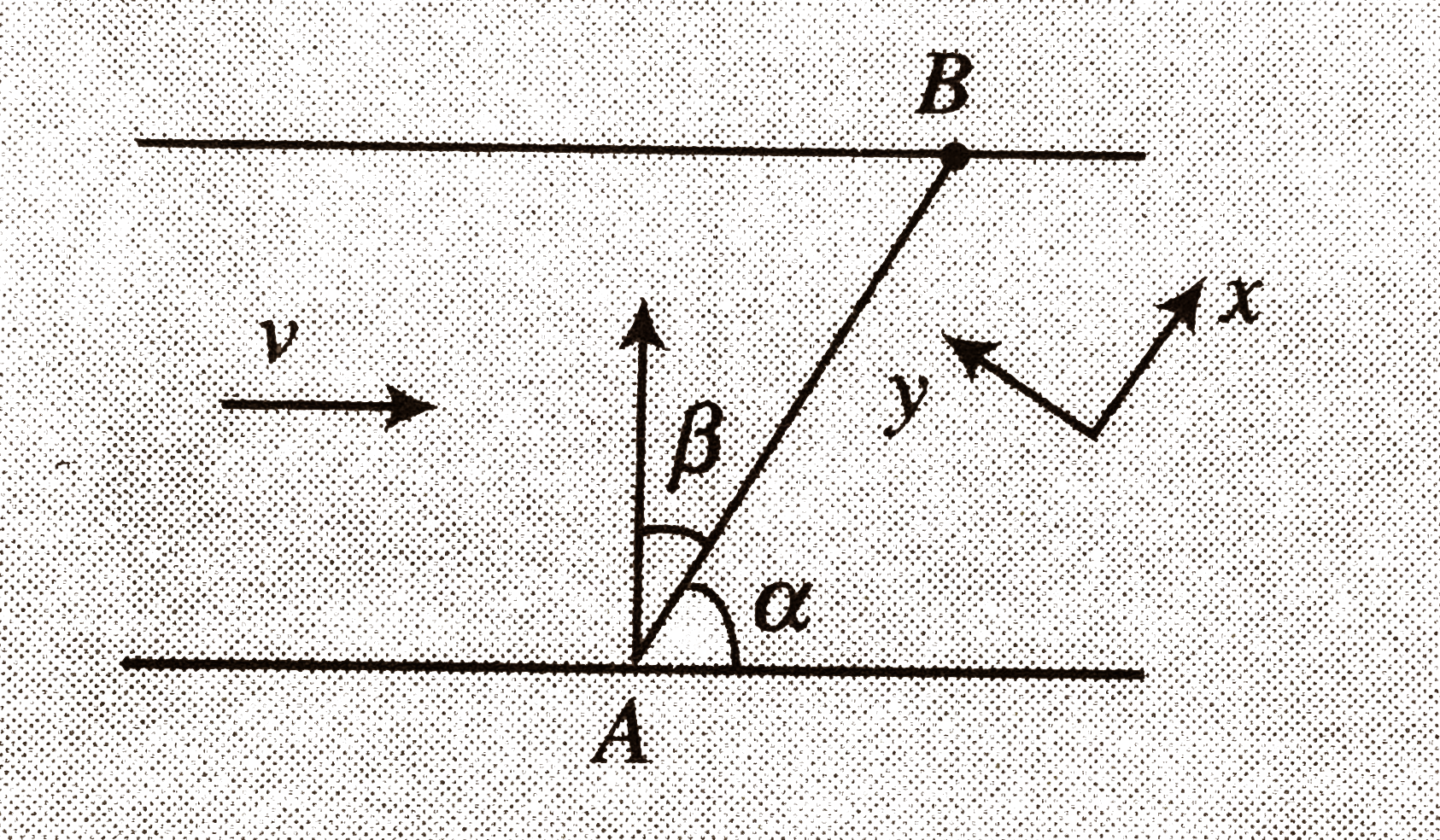 .
.
View SolutionVelocity of man w.r.t river is equal to velocity at river value of θ for which man reaches directly at B
View SolutionThe speed of river current close to banks is nearly zero. The current speed increases linearly from the banks to become maximum (=V0) in the middle of the river. A boat has speed ‘u’ in still water. It starts from one bank and crosses the river. Its velocity relative to water is always kept perpendicular to the current. Find the distance through which the boat will get carried away by the current (along the direction of flow) while it crosses the river. Width of the river is l.
View SolutionThe ratio of downstream drift of a person in crossing a river making same angles with downstream and upstream are respectively 2 : 1. The ratio of the speed of river u and the swimming speed of person v is:
View SolutionA man can swim with speed u with respect to river. The widith of river is d. The speed of the river is zero at the banks and increses linearly to V0 till mid stream of the river then decreases to zero to the other bank. When man crosses the river in shoetest time, drift is equal to: (givenu>v0)
View Solution
