Velocity of man w.r.t river is equal to velocity at river value of θ for which man reaches directly at B 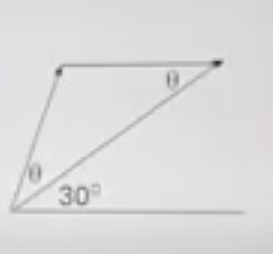
Step by step video & image solution for Velocity of man w.r.t river is equal to velocity at river value of theta for which man reaches directly at B by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
(A): Relative velocity of A w.r.t. B is greater than the velocity of either, when they are moving in opposite directions.
(R): The relative velocity between any two bodies is equal to the sum of the velocities of the two bodies.
View SolutionWidth of a river is 60m . A swimmer wants to cross the river such that he reaches from A to B directly. Point B is 45m ahead of line AC (perpendicular to river) Assume speed of river and speed of swimmer as equal. Swimmer must try to swim at angle θ with line AC .If the value of θ (in degrees) is N2 .Find N
View Solution
Knowledge Check
Velocity of water in a river is
ASame everywhereBMore in the middle and less near its banksCLess in the middle and more near its banksDIncrease from one bank to other bankAssertion: Relative velocity of A w.r.t B is greater than the velocity of either, when they are moving in opposite directions.
Reason: Relative velocity of A w.r.t B=→vA−→vBAIf both assetion and reason are true and the reason is the correct explanation of the assertion.BIf both assertion and reason are true but reason is not the correct explanation of the assertionCIf assertion is true but reason is falseDIf the assertion and reason both are false.A man swims across the river which flows with a velocity of 3 km/h due east. If the velocity of man relative to water is 4 km/h due north, then what is his velocity and its direction relative to the shore of the river?
A4 km/h, 63∘50' west of northB5 km/h, 36∘52' west of northC4 km/h, 63∘50' east of northD5 km/h, 36∘52' east of north
River-Man Situation
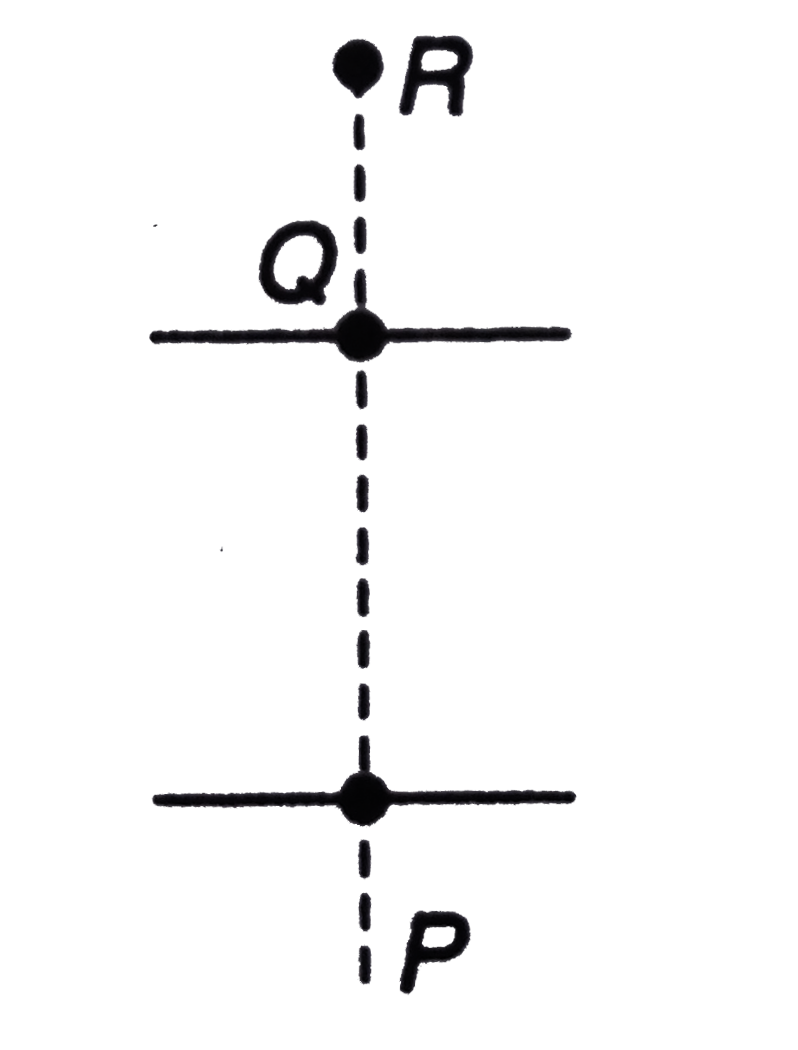
View SolutionA river of width ω is flowing with a uniform velocity v. A boat starts moving from point P also With velocity v relative to the river. The direction of resultant velocity is always perpendicular to the line joining boat and the fixed point R. Point Q is on the opposite side of the river. P, Q and R are in a straight line. If PQ=QR=ω, find (a) the trajectory of the boat, (b) the drifting of the boat and (c) the time taken by the boat to cross the river.
View SolutionA ,man wishing to cross a river flowing with velocity u jumps at an angle θ with the river flow.
(a) Find the net velocity of the man with respect to ground if he can swim with speed v in still water.
(b) In what direction does the boat actually move ?
( c) Find how far from the point directly opposite to the starting point does the boat reach the opposite bank, if the width of the river is d.
View SolutionSTATEMENT-1: A man can cross river of width d in minimum time t. On increasing river velocity, minimum time to cross the river by man will remain uncharged.
STATEMENT-2: Velocity of river is perpendicular to width of river. So time to cross the river is independent of velcoity of river.
View SolutionA trolley was moving horizontally on a smooth ground with velocity v with respect to the earth. Suddenly a man starts running from rear end of the trolley with a velocity (3/2)v with respect to the trolley. After reaching the other end, the man turns back and continues running with a velocity (3/2)v with respect to trolley in opposite direction. If the length of the trolley is L, find the displacement of the man with respect to earth when he reaches the starting point on the trolley. Mass of the trolley is equal to the mass of the man.
View Solution