A man of mass 100kg stands at the rim of a turtable of radius 2m and moment of inertia 4000kgm2 mounted on a vertical frictionless shaft at its centre. The whole system is initially at rest. The man now walks along the outer edge of the turntable with a velocity of 1m/s relative to the earth
a. With what angular velocity and in what direction does the turntable rotate?
b. Through what angle will it have rotated when the man reaches his initial position on the turntable?
c. Through what angle will it have rotated when the man reaches his initial position relative to the earth?
The table rotates through 2π/11 radians anticlockwise
The table rotates through 4π/11 radians clockwise
The table rotates through 4π/11 radians anticlock-wise
The table rotates through 27pi//11 radians clockwise
The correct Answer is:D
If the man completes one revolution relative to the table, then
θmt=2π
⇒2π=θm−θt
2π=θmt−ωtt (where t is the time taken)
t=2πωm−ωt=2π0.5−(−0.05)=2π0.55s
Angular displacement of the table is
θt=ωrt=−0.05×(2π0055)
=−(2π11) radians
The table rotates through 2π/11 radians clockwise.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct
142 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A man of mass m stands on a horizontal platform in the shape of a disc of mass m and radius R, pivoted on a vertical axis thorugh its centre about which it can freely rotate. The man starts to move aroung the centre of the disc in a circle of radius r with a velocity v relative to the disc. Calculate the angular velocity of the disc.

View SolutionA constant torque of 400Nm turns a wheel of moment of inertia 100kgm2 about an axis through its centre. The angular velocity gained in 4 second is
View Solution
Knowledge Check
A circular platform is mounted on a vertical frictionless axle. Its radius is r=2m and its moment of inertiaI=200kgm2. It is initially at rest. A 70kg man stands on the edge of the platform and begins to walk along the edge at speed v0=1ms−1 relative to the ground. The angular velocity of the platform is: a) 1.2 rad/s b) 0.4 rad/s c) 0.7 rad/s d) 2 rad/s
A1.2rads−1B0.4rads−1C0.7rads−1D2rads−1
The rotational kinetic energy of a disc is 450 J and its moment of inertia is 100 kg m2. What is its angular momentum ?
View SolutionA man of mass m=2kg is standing on a platform of mass M=5kg, then at any instant.
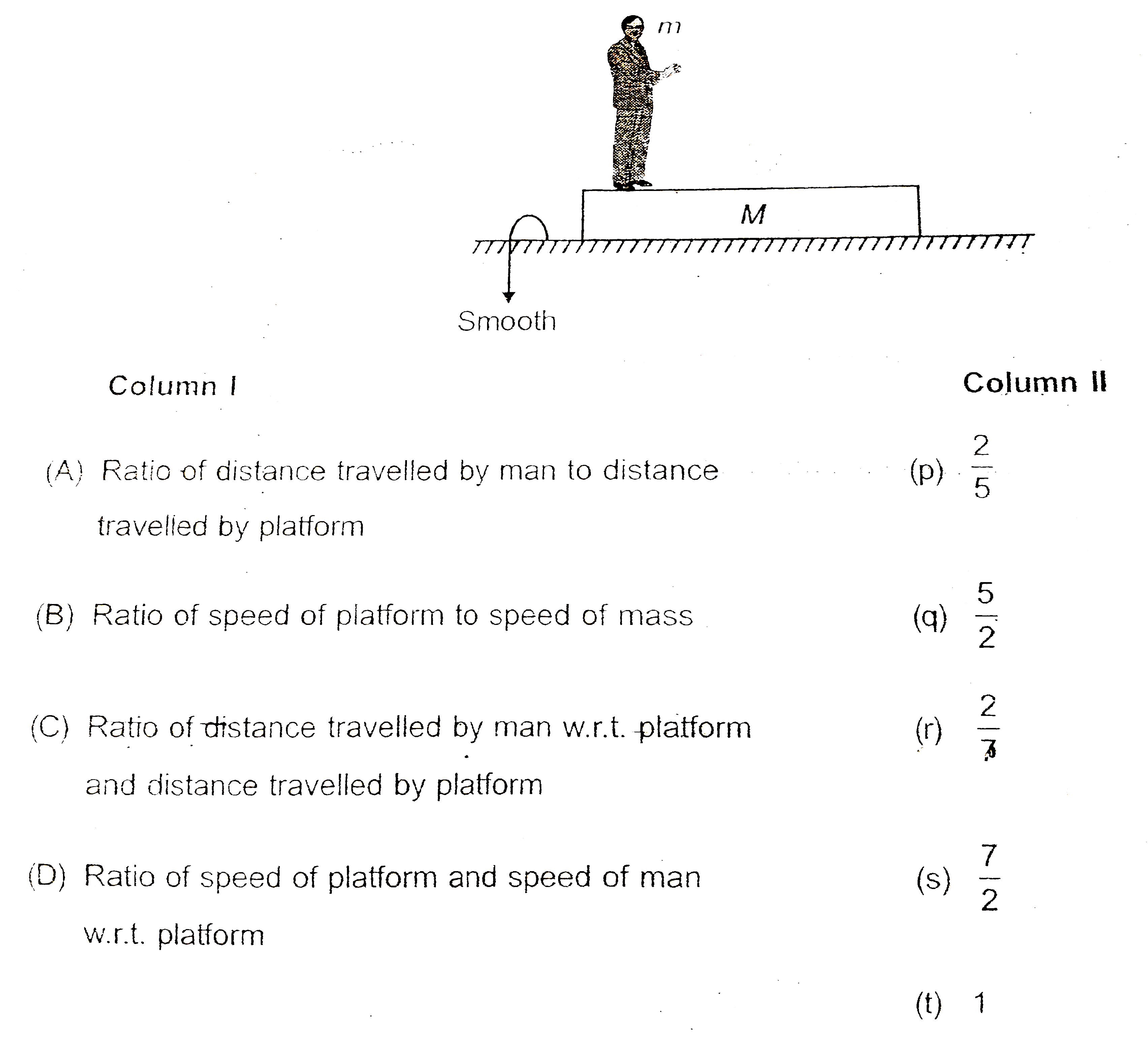
View SolutionA man of mass m is standing on a platform of mass M kept on smooth ice. If the man starts moving on the platform with a speed v relative to the platform with what velocity relative to the ice does the platform recoil?
View SolutionA string is wrapped around the rim of a wheel of moment of inertia 0.20 kg-m^2 and radius 20 cm. The wheel is free to rotate about it axis. Initially, the wheel is at rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 seconds.
View SolutionRain is falling vertically downward with velocity 4m/s. A man is moving horizontally with velocity 3m/s, the velocity of rain with respect to man is
View SolutionA wheel of radius 20 cm and moment of inertia 1 kgm^2 can rotate about its centre.A string is wrapped over its rim and is pulled by a force 'F' tangential to the rim of wheel.If angular acceleration produced is 2 rad/s^2 then the value of force 'F' is
View SolutionA constant torque of 1000N−m turns a wheel of moment of inertia 200kg−m2 about an axis through its centre. Its angular velocity after 3 seconds is.
View Solution
