A string is wrapped around the rim of a wheel of moment of inertia 0.20 kg-m^2 and radius 20 cm. The wheel is free to rotate about it axis. Initially, the wheel is at rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 seconds.
To solve the problem step by step, we will follow the principles of rotational mechanics.
Step 1: Identify Given Values
- Moment of inertia (I) = 0.20 kg·m²
- Radius of the wheel (R) = 20 cm = 0.20 m
- Force applied (F) = 20 N
- Time (t) = 5.0 seconds
- Initial angular velocity (ω₀) = 0 rad/s (since the wheel is initially at rest)
Step 2: Calculate the Torque (τ)
The torque (τ) exerted on the wheel by the force can be calculated using the formula:
τ=F×R
Substituting the values:
τ=20N×0.20m=4N⋅m
Step 3: Calculate the Angular Acceleration (α)
Using the relationship between torque and angular acceleration:
τ=Iα
We can rearrange this to find angular acceleration (α):
α=τI
Substituting the values:
α=4N⋅m0.20kg⋅m²=20rad/s²
Step 4: Calculate the Angular Velocity (ω) after 5 seconds
Using the formula for angular velocity:
ω=ω0+αt
Since the initial angular velocity (ω₀) is 0:
ω=0+(20rad/s²)×(5s)
Calculating this gives:
ω=100rad/s
Final Answer:
The angular velocity of the wheel after 5.0 seconds is 100 rad/s.
---
- Moment of inertia (I) = 0.20 kg·m²
- Radius of the wheel (R) = 20 cm = 0.20 m
- Force applied (F) = 20 N
- Time (t) = 5.0 seconds
- Initial angular velocity (ω₀) = 0 rad/s (since the wheel is initially at rest)
The torque (τ) exerted on the wheel by the force can be calculated using the formula:
τ=F×R
Substituting the values:
τ=20N×0.20m=4N⋅m
Using the relationship between torque and angular acceleration:
τ=Iα
We can rearrange this to find angular acceleration (α):
α=τI
Substituting the values:
α=4N⋅m0.20kg⋅m²=20rad/s²
Using the formula for angular velocity:
ω=ω0+αt
Since the initial angular velocity (ω₀) is 0:
ω=0+(20rad/s²)×(5s)
Calculating this gives:
ω=100rad/s
The angular velocity of the wheel after 5.0 seconds is 100 rad/s.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Objective -1
Explore 26 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Objective -2
Explore 14 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Questions for short Answer
Explore 21 Videos
- REST AND MOTION : KINEMATICSBook:HC VERMA ENGLISHChapter:REST AND MOTION : KINEMATICSExercise:Question for short Answer
Explore 13 Videos
- SIMPLE HARMONIC MOTIONBook:HC VERMA ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Question for short Answer
Explore 15 Videos
Similar Questions
A flywheel of moment of inertia 0.4 kg m2 and radius 0.2 m is free to rotate about a central axis. If a string is wrapped around it and it is pulled with a force of 10N. Then its angular velocity after 4s will be
View SolutionA wheel of moment of inertia 0.500kg−m2 and radius 20.0 cm is rotating about its axis at an angular speed of 20.0 rad/s. It picks up a stationary particle of mass 200 g at its edge. Find the new angular speed of the wheel.
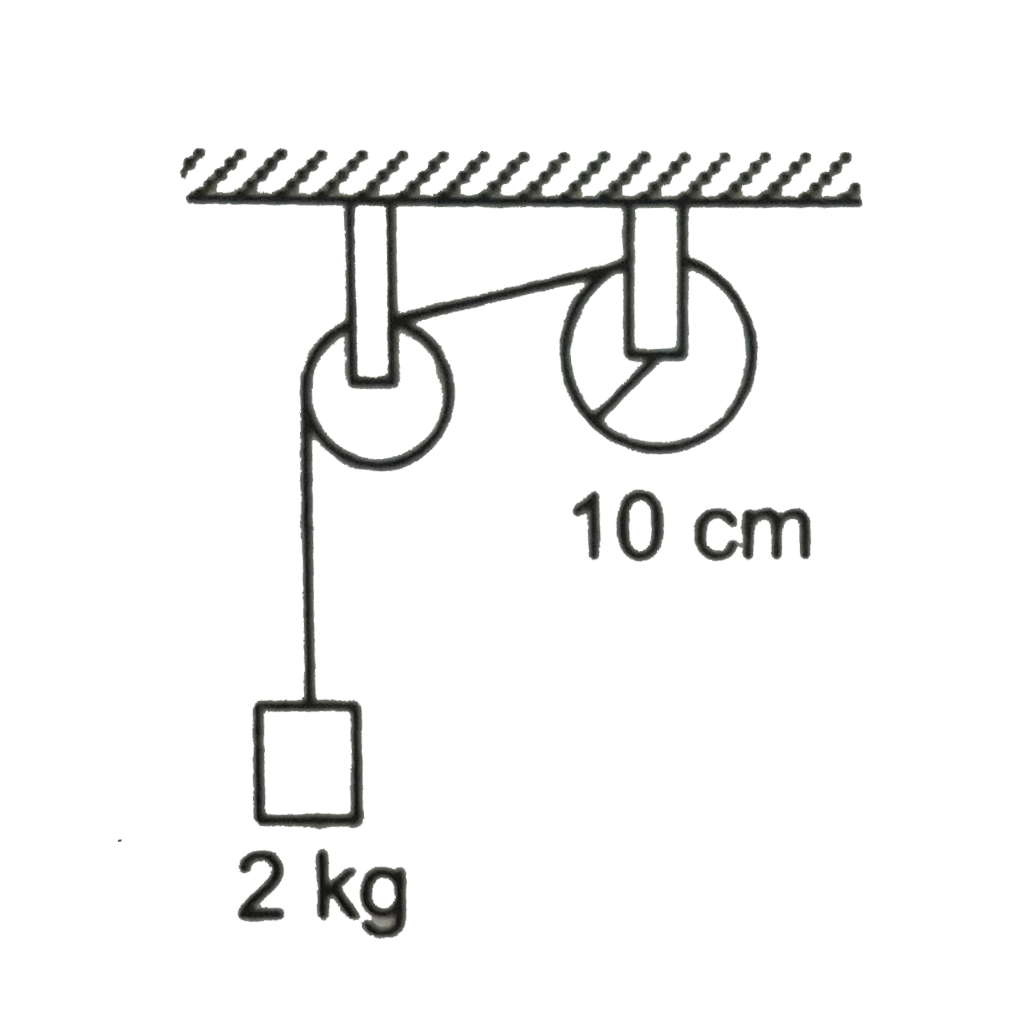
View SolutionA string is wrapped on a wheel of moment of inertia 0.20 kg-m^2 and radius 10 cm and goes through a light pulley to support a block of mass 2.0 kg as shown in figure. Find the acceleration of the block.
View SolutionA wheel having moment of inertia 2 kg m^2 about its axis, rotates at 50 rpm about this axis. Find the torque that can stop the wheel in one minute.
View SolutionA wheel of moment of inertia I and radius R is rotating about its axis at an angular speed ω. It picks up a stationary particle of mass m at its edge. Find the new angular speed of the wheel.
View SolutionA wheel of moment of inertial I and radius R is rotating about its axis at an angular speed ω. It picks up a stationary particle of mass m at its edge. Find the new angular speed of the wheel.
View SolutionA cord is wound around the circumference of wheel of radius r. The axis of the wheel is horizontal and MI is I. A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h, the angular velocity of the wheel will be
View SolutionA cord of negligible mass is wound round the rim of a flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
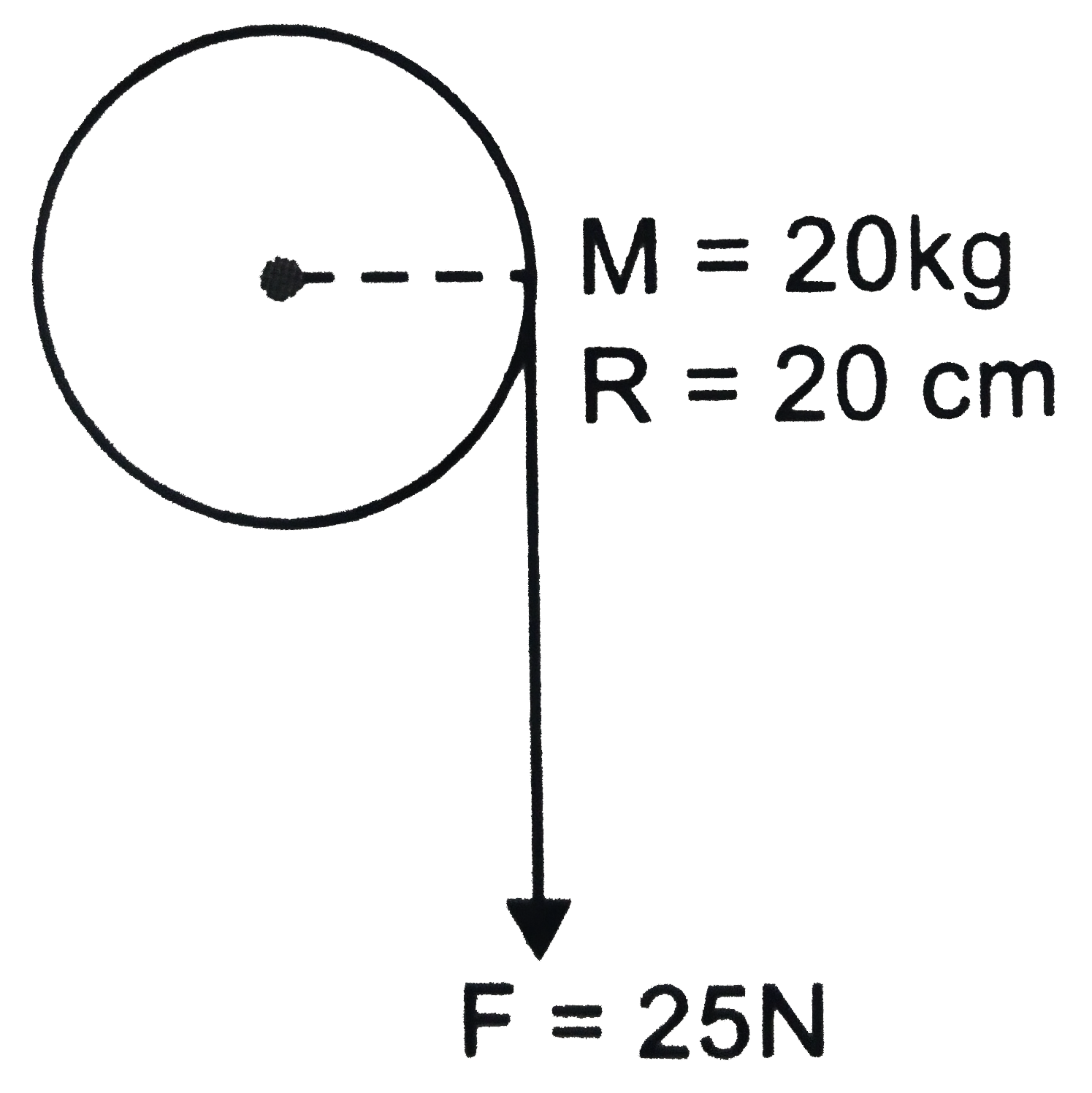
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).
View SolutionA constant torque of 1000N−m turns a wheel of moment of inertia 200kg−m2 about an axis through its centre. Its angular velocity after 3 seconds is.
View SolutionA flywheel of moment of inertia 2kg-m2 is rotated at a speed of 30rad/s. A tangential force at the rim stops the wheel in 15 second. Average torque of the force is
View Solution
