A man of mass m runs without sliding from rest from one end of a boat of mass M and length l with an acceleration a relative to the boat. If the friction between water and boat is neglected find the

a. acceleration of CM of the system (M+m)
b. acceleration of the man and boat
c. position of man at the time when he reaches to other end of the boat
d. frictional force
e. work done by friction on boat.
f. total work done by friction.
g. velocities of man and boat when the man reaches other end of the boat.
h. work down by man
Consider 'boat and man' a system. No external force acts on the system in horizontal direction and initially the system is at rest i.e., the centre of mass is at rest. The acceleration of centre of mass will be zero.
There will to be an displacement of centre of mass.
b. Considering the FBD of man and boat. If we consider man and boat separately, the static friction between man and boat will be responsible for the motion of man and boat but as a whole the friction will be an internal force and will not move centre of mass of system
Let the acceleration and displacement of man be →amand→xm and that for boat be →aMand→xM.
→am=→am,M+→aM=−aˆi+aMˆi
=(aM−a)ˆi

But →acm=m→am+M→aM(m+M)
or 0=m(aM−a)ˆi+MaMˆi(m+M)
⇒→aM=ma(m+M)(ˆi) (towards right)
Hence am=ma(m+M)−a
⇒→am=Ma(m+M)(−ˆi) (towards left)
c. We know the displacement of CM
→xCM=m→xM+M→xM(m+M)
Here →xm=→xm,M+→xM=(−lˆi+xMˆi)
⇒→xm=(xM−l)ˆi
Hence xcm=O=m(xM−l)ˆi+MxMˆi(m+M)
⇒→–––(M)=−ml(m+M)(ˆi)[towards right]
and →xm=−Ml(m+M)(ˆi) [towards left]
position of man from observer at the time when the man reaches to other end of the boat.
→x=(x0+l)ˆi+→xm
=(x0+l)ˆi−Ml(m+M)ˆi=(x0+ml(m+M))ˆi
d. From FBD of man friction force acting on the man,
f=mam=m(ma(m+m))=Mma(m+M)
e. Work done by friction force on boat
(Wf)boat=→f→xm=[Mma(m+M)][ml(m+M)]
⇒(Wf)boat=Mm2al(m+M)2
f. As friction between man and boat in static nature and total work done by static friction force on the system should be zero
g. For finding the velocity of man when he reaches other end of the boat, we can use kinematics
Using v2m=u2m+2amxm=0+2(Ma(m+M))(Ml(m+M))
⇒v2m=(Mm+M)2.2al
Hence velocity of man vM=(Mm+M)√2al
Similarly velocity of boat vM=(mm+M)√2al
h. if we consider man + boat on system, friction will do no work on system as it in static nature. but we can se the kinetic energy of the system will increase. the question a rises here who does work to increase the kinetic energy of system. the answer is man. the man does this work through his internal energy to increase the kinetic energy of the system.
Using work energy theorem on the system we get
Wman+Wfriction=△K=K−Kf−Ki
We know Wfriction=0
Wman+0=(12mv2m+12MV2m)−0
Vman=12m[(Mm+M)22al]+12M[(m(m+M)22al]−0
⇒Wman=mMal(m+M)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples
13 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A man of mass m walks from end A to the other end B of a boat of mass M and length l. The coefficient of friction between the man and the boat is μ an neglect any resistive force between the boat and the water.
View SolutionA plank of mass m rests symmetrically on two wedges B and C of mass M. What is the acceleration of the plank? Neglect friction between all the contact surfaces.

View SolutionA man of 80 kg attempts to jump from the small boat of mass 40 kg on to the shore. He can generate a relative velocity of 6 m/s between him and boat. His velocity towards shore is
View SolutionStarting from rest at s=0,a boat travels in a straight line with an acceleration on as shown by the a-s graph. Determine the boat's speed at s=40,90 .

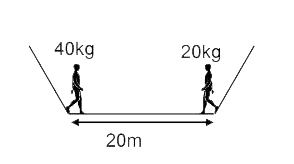
View SolutionTwo men of masses 40 kg and 20 kg are standing on a boat of mass 100 kg. Length of boat is 20m. Neglect the friction between water and boat. Find the displacement of the boat when both the persons reach at middle of boat.
View SolutionA man of mass m moves with a constant speed on a plank of mass M and length l kept initially at rest on a frictionless horizontal surface, from one end to the other in time t. The speed of the plank relative to grounud while man is moving, is
View SolutionA man of mass m moves with a constant speed on a plank of mass M and length L kept initially at rest on a frictionless horizontal surface . From one end to the other he reaches in time t . The speed of the plank relative to ground while man is moving , is
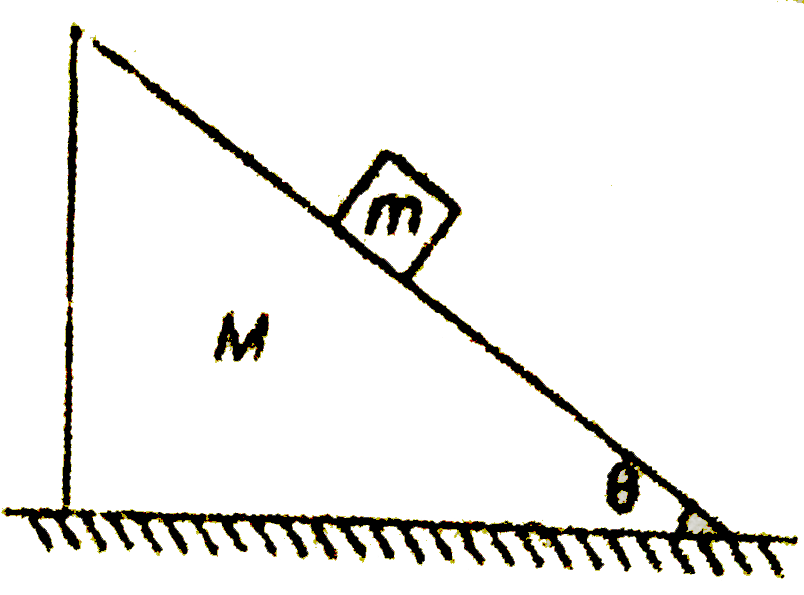
View SolutionA block of mass m slides down on a wedge of mass M as shown in figure .Let a1 be the asseleration of the acceleration of and a2 the the acceleration od block 1N1 is the normal reaction between block and wedge and N2 the normal reaction between wedge and gound .frication is absent everwhere .Select the correct alternative(s)
View SolutionA man of mass m is standing at one end of of a plank of mass M. The length of the plank is L and it rests on a frictionless horizontal ground. The man walks to the other end of the plank. Find displacement of the plank and man relative to the ground.

View SolutionA boy of mass 30 kg is standing at one end on a stationary boat over a lake. The boat has a mass 70 kg and length 10 m. Now the boy walked to the other end of the boat. Relative to the ground
View Solution
