A man of 80 kg attempts to jump from the small boat of mass 40 kg on to the shore. He can generate a relative velocity of 6 m/s between him and boat. His velocity towards shore is
(a)4ms−1
(b)8ms−1
(c)2ms−1
(d)3ms−1
The correct Answer is:C
To solve the problem step by step, we will use the principle of conservation of momentum and the concept of relative velocity.
1. Identify the Given Data:
- Mass of the man, mm=80kg
- Mass of the boat, mb=40kg
- Relative velocity of the man with respect to the boat, Vmb=6m/s
2. Define the Variables:
- Let Vm be the velocity of the man towards the shore.
- Let Vb be the velocity of the boat in the opposite direction (away from the shore).
3. Use the Relative Velocity Equation:
The relative velocity of the man with respect to the boat is given by:
Vmb=Vm−Vb
Rearranging this gives:
Vm=Vmb+Vb
4. Apply Conservation of Momentum:
Since there are no external forces acting on the system, the total momentum before and after the jump must be conserved. Initially, both the man and the boat are at rest, so the initial momentum is zero:
0=mmVm+mb(−Vb)
Here, we take the velocity of the boat as negative because it moves in the opposite direction to the man.
5. Substituting Values:
Rearranging the momentum equation gives:
mmVm=mbVb
Substituting the masses:
80Vm=40(−Vb)
Simplifying this gives:
2Vm=−Vb(1)
6. Substituting into the Relative Velocity Equation:
From equation (1), we can express Vb in terms of Vm:
Vb=−2Vm
Now substitute this into the relative velocity equation:
Vm=6+(−2Vm)
Rearranging gives:
Vm+2Vm=6
3Vm=6
Therefore:
Vm=63=2m/s
7. Conclusion:
The velocity of the man towards the shore is Vm=2m/s.
Final Answer:
The velocity of the man towards the shore is 2 m/s.
- Mass of the man, mm=80kg
- Mass of the boat, mb=40kg
- Relative velocity of the man with respect to the boat, Vmb=6m/s
- Let Vm be the velocity of the man towards the shore.
- Let Vb be the velocity of the boat in the opposite direction (away from the shore).
The relative velocity of the man with respect to the boat is given by:
Vmb=Vm−Vb
Rearranging this gives:
Vm=Vmb+Vb
Since there are no external forces acting on the system, the total momentum before and after the jump must be conserved. Initially, both the man and the boat are at rest, so the initial momentum is zero:
0=mmVm+mb(−Vb)
Here, we take the velocity of the boat as negative because it moves in the opposite direction to the man.
Rearranging the momentum equation gives:
mmVm=mbVb
Substituting the masses:
80Vm=40(−Vb)
Simplifying this gives:
2Vm=−Vb(1)
From equation (1), we can express Vb in terms of Vm:
Vb=−2Vm
Now substitute this into the relative velocity equation:
Vm=6+(−2Vm)
Rearranging gives:
Vm+2Vm=6
3Vm=6
Therefore:
Vm=63=2m/s
The velocity of the man towards the shore is Vm=2m/s.
The velocity of the man towards the shore is 2 m/s.
Similar Questions
A man of mass m runs without sliding from rest from one end of a boat of mass M and length l with an acceleration a relative to the boat. If the friction between water and boat is neglected find the

a. acceleration of CM of the system (M+m)
b. acceleration of the man and boat
c. position of man at the time when he reaches to other end of the boat
d. frictional force
e. work done by friction on boat.
f. total work done by friction.
g. velocities of man and boat when the man reaches other end of the boat.
h. work down by man
View SolutionA man of mass 80 kg is riding on a small cart of mass 40 kg which is rolling along a level floor at a speed 2 m/s . He is running on the cart , so that his velocity relative to the cart is 3 m/s in the direction opposite to the motion of cart . What is the speed of the centre of the mass of the system ?
View SolutionA marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
View SolutionA marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
View SolutionA man of mass 60kg jumps from a trolley of mass 20kg standing on smooth surface with absolute velocity 3m/s. Find velocity of trolley and total energy produced by man.
View SolutionA bullet of mass 40 g is fired from a gun of mass 10 kg. If velocity of bullet is 400 m/s. then the recoil velocity of the gun wil be
View SolutionA man of mass 80kg pushes box of mass 20kg horizontaly. The man moves the box with a constant acceleration of 2m/s2 but his foot does not slip on the ground. There is no friction between the box and the ground. There is no friction between the box and the ground. whereas there is sufficient friction between the man's foot and the ground to prevent him from slipping.
Assertion:- The force applied by the man on the box is equal and opposite to the force applied by the force applid by the box on the man.
Reason:- Friction force applied by the ground on the man is 200N.
View SolutionFrom a rifle of mass 4kg, a bullet of mass 50g is fired with an initial velocity of 35m/s. Calculate the initial recoil velocity of the rifle.
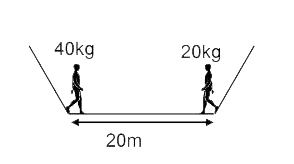
View SolutionTwo men of masses 40 kg and 20 kg are standing on a boat of mass 100 kg. Length of boat is 20m. Neglect the friction between water and boat. Find the displacement of the boat when both the persons reach at middle of boat.
View SolutionTwo particles of mass 1 kg and 3 kg move towards each other under their mutual force of attraction. No other force acts on them. When the relative velocity of approach of the two particles is 2m/s, their centre of mass has a velocity of 0.5 m/s. When the relative velocity of approach becomes 3m/s, the velocity of the centre of mass is 0.75 m/s.
View Solution