A man rides a jet boat with a speed of 40km/hr in the north -east direction and the shore line makes an angle of 10∘ south of east . Find the component of the velocity of the jet boat
(i) along the shoreline and
(ii) perpendicular to the shoreline .
To solve the problem, we need to find the components of the velocity of the jet boat in two directions: along the shoreline and perpendicular to the shoreline.
1. Identify the Given Information:
- Speed of the jet boat, v=40km/hr
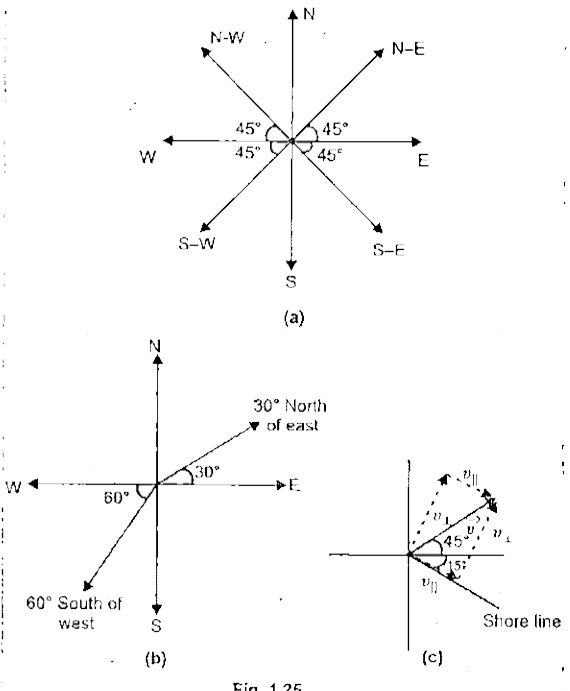
- Direction of the jet boat: North-East (which is at an angle of 45∘ from the East).
- The angle of the shoreline with respect to the East: 10∘ South of East.
2. Determine the Total Angle:
- The angle between the direction of the jet boat and the shoreline can be calculated. The jet boat is at 45∘ (North-East) and the shoreline is at 10∘ (South of East).
- Therefore, the angle between the jet boat's direction and the shoreline is:
Total angle=45∘+10∘=55∘
3. Calculate the Component of Velocity Along the Shoreline:
- The component of the velocity along the shoreline can be found using the cosine of the angle:
valong=v⋅cos(Total angle)=40⋅cos(55∘)
- Using a calculator, we find:
cos(55∘)≈0.5736
- Therefore:
valong=40⋅0.5736≈22.94km/hr
4. Calculate the Component of Velocity Perpendicular to the Shoreline:
- The component of the velocity perpendicular to the shoreline can be found using the sine of the angle:
vperpendicular=v⋅sin(Total angle)=40⋅sin(55∘)
- Using a calculator, we find:
sin(55∘)≈0.8192
- Therefore:
vperpendicular=40⋅0.8192≈32.77km/hr
Final Answers:
(i) The component of the velocity of the jet boat along the shoreline is approximately 22.94 km/hr.
(ii) The component of the velocity of the jet boat perpendicular to the shoreline is approximately 32.77 km/hr.
- Speed of the jet boat, v=40km/hr
- Direction of the jet boat: North-East (which is at an angle of 45∘ from the East).
- The angle of the shoreline with respect to the East: 10∘ South of East.
- The angle between the direction of the jet boat and the shoreline can be calculated. The jet boat is at 45∘ (North-East) and the shoreline is at 10∘ (South of East).
- Therefore, the angle between the jet boat's direction and the shoreline is:
Total angle=45∘+10∘=55∘
- The component of the velocity along the shoreline can be found using the cosine of the angle:
valong=v⋅cos(Total angle)=40⋅cos(55∘)
- Using a calculator, we find:
cos(55∘)≈0.5736
- Therefore:
valong=40⋅0.5736≈22.94km/hr
- The component of the velocity perpendicular to the shoreline can be found using the sine of the angle:
vperpendicular=v⋅sin(Total angle)=40⋅sin(55∘)
- Using a calculator, we find:
sin(55∘)≈0.8192
- Therefore:
vperpendicular=40⋅0.8192≈32.77km/hr
(i) The component of the velocity of the jet boat along the shoreline is approximately 22.94 km/hr.
(ii) The component of the velocity of the jet boat perpendicular to the shoreline is approximately 32.77 km/hr.
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - COMPETITION FILE OBJECTIVE TYPE QUESTIONS (A. Multiple Choice Questions)
30 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - COMPETITION FILE OBJECTIVE TYPE QUESTIONS (B. Multiple Choice Questions)
38 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Revision Exercises (Long Answer Question)
6 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
A man rides a jet boat with a speed of 40km/hr in the north -east direction and the shore line makes an angle of 10∘ south of east . Find the component of the velocity of the jet boat
(i) along the shoreline
(ii) perpendicular to the shoreline.
View SolutionA man rows a boat with a speed of 18Kmh−1 in the north-west direction (figure). The shoreline makes an angle of 15∘ south of west. Obtain the components of the velocity of the boat along the shoreline and perpendicular to the shoreline.

View Solution
Knowledge Check
A man rows a boat with a speed of 18 km/hr in northwest direction. The shoeline makes an angle of 15∘ south of west. Obtain the component of the velocity of the boat along the shoreline:
A9 km/hrB18√32 km/hrC18cos15∘ km/hrD18cos75∘ km/hrA car A going north-east at 80km/h and another car B is going south-east at 60km/h. The direction of the velocity of A relative to B makes an angle with the north equal to:
Atan−1(2/7)Btan−1(7/2)Ctan−1(7)Dtan−1(1/7)
A man rows a boat with a speed 10 m/s along N-E direction. The shore line is 15∘ south of east. . What are components of the velocity vector along and perpendicular to shore?
View SolutionThe velocity of a body is 100kmh−1, 30^(@) west of south . Find the north ad east components of the vector.
View SolutionA motor boat is racing towards North at 25km/h and the water current in that region is 10km/h in the direction of 6000 East of South. Find the resultant velocity of the boat.
View SolutionAn aeroplane takes off at an angle of 60∘ to the vertical .If the component of velocity along the vertical is 250km/hr, calculate its
(i) actual velocity and
(ii) horizontal component of velocity.
View Solution47.A man moves 10m in a direction of 37^(@) East of North then 5sqrt(2)m in South-East direction and finally 20m in a direction of 53^(@) South of West.Find the magnitude of resultant displacement of man?
View SolutionA body is travelling due east at a speed of 15km/h for one hour and then turns towards south at a speed of 10km/h for one hour. Find the average velocity of the body.
View Solution
